統計的検定の考え方を説明しました。
小テスト
「Google One VPN」を2024年中に提供終了
-
Googleは、有料サービス「Google One」の加入者向けに提供しているVPNサービス「Google One
VPN」を2024年中に提供終了する。 ■Google One VPNを2024年中に提供終了 （Goo...
2012-10-25
PowerPointの使い方
今日は、パソコンに保存したファイルの探し方を説明した後、
情報実習室利用の手引き 6.3 PowerPoint2010 を使うを見ながら何か一つテーマを決めて、それを紹介するパワーポイントを作ってメールに添付して提出してください。条件として
情報実習室利用の手引き 6.3 PowerPoint2010 を使うを見ながら何か一つテーマを決めて、それを紹介するパワーポイントを作ってメールに添付して提出してください。条件として
- 一枚目はタイトルです。自分が紹介するテーマと、学籍番号、名前を書いてください。
- 二枚目は目次です。3枚目以降の内容を箇条書きで書いてください。
- 三枚目以降が具体的な紹介です。
- 写真や図などを少なくとも一つ貼り付けてください。
- 数式を少なくとも一回使ってください。
- アニメーションを少なくとも一回使ってください。
2012-10-21
Bluetooth PAN
PANはPersonal Area Networkの略で、無線LANと似たようなことをBluetoothで行います。
スマートフォンで無線LAN(WiFi)テザリングするよりも、消費電力が少ないです。
また、人が多いところでWiFiテザリングすると、無線LANが混信して安定して使えないことがあります。
そんな時は、USBで直接繋ぐのが一番確実ですが、USBケーブルを持っていない場合、Bluetooth PANでもWiFiよりは混信が少ないです。
但しWiFiよりも遅いですが、Bluetoothも速くなっているので3GならBluetoothの速度が問題になることは無いでしょう。
スマートフォンで無線LAN(WiFi)テザリングするよりも、消費電力が少ないです。
また、人が多いところでWiFiテザリングすると、無線LANが混信して安定して使えないことがあります。
そんな時は、USBで直接繋ぐのが一番確実ですが、USBケーブルを持っていない場合、Bluetooth PANでもWiFiよりは混信が少ないです。
但しWiFiよりも遅いですが、Bluetoothも速くなっているので3GならBluetoothの速度が問題になることは無いでしょう。
私にとって一番のメリットは、PHSによるパケット通信が基本使用料だけで使えるHybrid W-ZERO3がBluetooth PANには対応していることです。
WiFiも使えますが、ad hoc接続に限定されるのでAndroidを(root化しない限り)繋げません。
Androidも以前はBluetoothが使えてもPANまでは使えない機種が多く、root化が必要でしたが、4.0になってからはOS標準でBluetoothテザリングに対応するようになったので、PANに対応する機種が増えました。
auのHTC EVO 3DはAndroid2.3では対応していませんが
4.0にバージョンアップするとPANにも対応します。
ところがHTC EVO 3DはPANのアクセスポイントにはなれますが、他のアクセスポイントに接続してインターネットは使えないようです。
WS027SHとはHybrid W-ZERO3のことです。
使えるならばこのように表示される筈です。
これで繋がることは確認できました。
googleのヘルプを見ると
> [設定] > [無線とネットワーク] > [その他] > [テザリングとポータブルアクセスポイント] に移動します。
> [Bluetoothテザリング] チェックボックスをオンにします。
と書かれていますが、これは自身がアクセスポイントになるための設定です。
Nexus7は対応しているのですが、品切れで入手できません。
ただ、肝心のPHSパケット通信の速度が、電波状況の良いところでは220kbpsになったこともあって、b-mobile U300と違ってyoutubeなどの制限もないので、これならU300並みに使えるのですが、場所によっては(というかアンテナが減ったらしく大抵のところで)60~80kbps程度で、これだとイオンで売っている毎月980円のb-mobile SIMの方が安くて速いです。
今となっては全く繋がらないよりはマシ、という程度です。
日本通信b-mobile4G/LTE Amazon限定SIMレビュー：iPhone4S SIMフリー、OptimusLTE L-01Dでもテザリング可能
2012-10-18
統計的検定
前回に引き続き、統計学Iの教科書の例題を、Excelを使って計算します。
出典
11.5
12.0
11.0
12.5
13.0
11.5
13.5
12.5
13.0
12.5
対立仮説:μ<13
母分散も分からないのでデータから推定する⇒推定するのでVARを使う(VARPではない)
母分散を不偏分散で推定するのでt統計量を計算する(統計学の範囲)
は標本平均なのでAVERAGE関数で計算できます。
μは検定したい母平均の値なので13です。 U2は不偏分散なのでVAR関数で計算できます。
nは観測値の数なので10です。
平方根はSQRTです。
これらの関数を用いて、上の式で与えたtの値を計算してみてください。
-2.80624304になったら正解です。
帰無仮説:μ=0
対立仮説:μ≠0
t=3.14485451になります。
例4.8では、平均μは13に等しいかもっと小さいか、の検定でした。
今回は、平均μは0に等しいかことなるか、の検定なので
P(t≦-3.14485451 または 3.14485451≦t)の値を求めます。
このような両側検定用の関数も用意されていますがあれこれ覚えるのも面倒ですし左右対称ですので
P(t≦-3.14485451)を求めて2倍します。
計算すると0.013704454なので約1.37%であり、これは有意水準2%よりも小さいので帰無仮説を棄却します。
等しいという帰無仮説を棄却しないなら、母分散が等しい場合の検定を行う。
等しいという帰無仮説を棄却したならば、母分散が等しくない場合の検定を行うが、これは統計学IIの内容。
帰無仮説:σX2=σY2
対立仮説:σX2≠σY2
σX2とσY2をそれぞれ不偏分散UX2, UY2で推定して
の値が大きすぎる時と小さすぎる時に棄却します。
分散に差がなければFの値は1前後になる筈です。
不偏分散を計算する関数を用いて計算するとF=1.710594315となります。
この値は1より大きいので、有意水準5%を、大きすぎる方と小さすぎる方に均等に割り振って、
P(F≧1.710594315)が2.5%より小さければ帰無仮説を棄却します。
男性10人、女性9人なのでFの確率分布はそれぞれ1を引いて自由度(9,8)のF分布なので、
P(F≧1.710594315)は =F.DIST.RT(1.710594315,9,8) で計算します。
この値は0.230633499なので、今回の結果は帰無仮説が正しくても約23%の確率で起こる、珍しくない事なので、帰無仮説を棄却しません。U_X^2%2b(n-1)U_Y^2}{m%2bn-2})
で推定できます。
U^2}})
は自由度m+n-2のt分布に従うので、これまでの例と同様に計算して、t=2.546316792となり、このようなことが起こる確率は0.02086737なので棄却します。
出典
母平均の検定
例4.8
次の値は、燃費が13km/ℓと称して売られている車で、実際に買った人が測った燃費である。この車の本当の燃費μが13なのかもっと小さいのかを有意水準5%で検定する。11.5
12.0
11.0
12.5
13.0
11.5
13.5
12.5
13.0
12.5
検定方法
帰無仮説:μ=13対立仮説:μ<13
母分散も分からないのでデータから推定する⇒推定するのでVARを使う(VARPではない)
母分散を不偏分散で推定するのでt統計量を計算する(統計学の範囲)
計算
μは検定したい母平均の値なので13です。 U2は不偏分散なのでVAR関数で計算できます。
nは観測値の数なので10です。
平方根はSQRTです。
これらの関数を用いて、上の式で与えたtの値を計算してみてください。
-2.80624304になったら正解です。
次に、この値が、仮に帰無仮説が正しかったらどれくらい起こりにくいことなのかを計算します。
P(t≦-2.80624304)を計算します。
tの確率分布は自由度9のt分布なので(統計学の範囲)ExcelのT.DIST関数を使います。
TとDISTの間にピリオドが入っていることに気を付けてください。
この関数はExcel2010以降でしか使えません。
P(t≦-2.80624304)の値は=T.DIST(-2.80624304, 9, TRUE)で計算できます。
9は自由度でTRUEは分布関数の値を計算する指示です。
FALSEにすると密度関数になります。
この値は0.010251238になるので、
帰無仮説が正しいなら約1.025%の確率でしか発生しない珍しいこと
だと分かります。
有意水準5%ということは、発生確率が5%より小さいことが起こったら帰無仮説を棄却するということなので、今回は母平均μ=13を棄却して、母平均はもっと小さいと判断します。
有意水準を1%にすると、今回は約1.025%の確率で発生するので棄却しません。
対応がある場合の二つの母集団の母平均の差の検定
例4.9
次の数字は、9名に関して安静時の最高血圧と入浴後の最高血圧である。血圧に変化はあるかを有意水準2%で検定する。| 安静時 | 入浴後 |
|---|---|
| 134 | 139 |
| 126 | 130 |
| 132 | 141 |
| 119 | 117 |
| 136 | 140 |
| 128 | 129 |
| 120 | 134 |
| 109 | 111 |
| 122 | 130 |
検定方法
入浴後－安静時の値の母平均μが0に等しいか異なるかを検定する。帰無仮説:μ=0
対立仮説:μ≠0
計算
9名それぞれに関して入浴後－安静時を計算して、例4.8と同様に計算するとt=3.14485451になります。
例4.8では、平均μは13に等しいかもっと小さいか、の検定でした。
今回は、平均μは0に等しいかことなるか、の検定なので
P(t≦-3.14485451 または 3.14485451≦t)の値を求めます。
このような両側検定用の関数も用意されていますがあれこれ覚えるのも面倒ですし左右対称ですので
P(t≦-3.14485451)を求めて2倍します。
計算すると0.013704454なので約1.37%であり、これは有意水準2%よりも小さいので帰無仮説を棄却します。
対応がない場合の二つの母集団の母平均の差の検定と、等分散の検定
手順
最初に、二つの母集団の母分散が等しいか検定する。等しいという帰無仮説を棄却しないなら、母分散が等しい場合の検定を行う。
等しいという帰無仮説を棄却したならば、母分散が等しくない場合の検定を行うが、これは統計学IIの内容。
例4.10
男性10人と女性9人の尿酸値は等しいかを有意水準5%で検定する。| 男性X | 女性Y |
|---|---|
| 4.7 | 3.9 |
| 6.3 | 4.8 |
| 5.8 | 5.1 |
| 5.1 | 3.5 |
| 3.4 | 4.9 |
| 4.9 | 3.8 |
| 5.4 | 4.2 |
| 4.6 | 5.0 |
| 5.7 | 3.5 |
| 6.1 |
等分散の検定
男性、女性のそれぞれの母分散をσX2, σY2として帰無仮説:σX2=σY2
対立仮説:σX2≠σY2
σX2とσY2をそれぞれ不偏分散UX2, UY2で推定して
分散に差がなければFの値は1前後になる筈です。
不偏分散を計算する関数を用いて計算するとF=1.710594315となります。
この値は1より大きいので、有意水準5%を、大きすぎる方と小さすぎる方に均等に割り振って、
P(F≧1.710594315)が2.5%より小さければ帰無仮説を棄却します。
男性10人、女性9人なのでFの確率分布はそれぞれ1を引いて自由度(9,8)のF分布なので、
P(F≧1.710594315)は =F.DIST.RT(1.710594315,9,8) で計算します。
この値は0.230633499なので、今回の結果は帰無仮説が正しくても約23%の確率で起こる、珍しくない事なので、帰無仮説を棄却しません。
平均の差の検定
二つの母集団の共通の母分散は
終わるのが遅くなって、教室を出たらもう陽が沈んでいました。
絞ったままの設定で撮ってしまって、感度がISO5000まで上がってしまいノイズが増えました。
2012-10-16
DSC-RX100
歪曲収差補正を止められる現像ソフトDxOを使って、広角端の歪曲収差を調べてみました。
カメラ自身で記録したJPEG
しかし位相差AFのNikon1と比べると、Nikon1ならピントが合う筈の被写体で合わないことがあります。
例えば(普通は撮りませんが説明用の例として)青空を背景に電線が一本渡っている場合に、電線にピントを合わせることができませんでした。
電線は撮りませんけど、飛行機雲で困りそうですし、コーヒーカップの中のコーヒーとカップの境界線にも合わせられません。
飛行機雲なら無限遠ですので適当な遠くのものでAFロックかけるという手がありますが、近くのものだと、「Nikon1(に限らず位相差AF)なら簡単に合わせられるのに」と思いながらマニュアルフォーカスすることになります。
そういう場合はRX100に限らずコントラストAFを使うコンデジやミラーレスだとどれも合わないのですが。
また、日暮れ後の風景など、暗くてAF補助光も届かない場合のピンボケ率も高いです。
オートフォーカスくらいはNikon1が勝たないと、RX100と比べて大きい、標準ズームだと暗い、同じ感度で同じ大きさにリサイズするとノイズが多い、ではNikon1の存在意義が危なくなります。
とは言え、ピントが合わなければ、どんなに画素が多くても、ノイズが少なくても意味ないですから、Nikon1の大きさで構わないならNikon1の方が良いと思います。
コントラストAFでもピントを合わせやすいものにピントを合わせる時間を比較して「コントラストAFでも位相差AFと合焦時間がほとんど変わらなくなった」と言われますが、それ以前の問題として、ピントを合わせることが出来る被写体が違いますので、Nikon1にも色々不満はありますが、Nikon1の大きさでも持ち歩ける時はNikon1を使うことになります。
プログラムAEでプログラムシフトを使わないと広角端で1/100 F1.8になりました。
コンデジとしてはセンサーが大きいので、特にマクロだと開放では被写界深度が浅すぎますし、収差も酷くはありませんが少しは絞った方が良いです。
あまり詳しくない人に「予算が許すならこれが一番！」と勧めましたが「全体にピントが合わせられずにボケてしまう」と言われてしまいました。
手振れ補正もありますし高感度ノイズもコンデジとしては少ないので、換算焦点距離分の1までシャッター速度を下げるなりISO400程度まで感度を上げて絞る露出プログラムが良いと思います。
マクロなら特に絞った方が良いと思うのですが、シーンセレクトでマクロを選んでも、感度を上げる前に絞りが開放になります。
結局、絞り優先AEに切り替えて自分で絞るか、感度を手動で上げるか、プログラムシフトを使う必要があり、初心者がカメラ任せでは他のコンデジより綺麗に撮れるとは限りません。
凄く暗いところなら絞り開放しか選択肢がないので、センサーの性能、レンズの明るさという基礎能力で他のコンデジに勝てますが、明るいところだと他のデジカメでは全体にピントが合わせられるのに、この機種でカメラ任せだとピントを合わせた部分以外ボケてしまうことになります。
この点、ニコンの一眼レフのオートモードは、カメラ任せでカメラの画質をほぼ引き出せます。
わざとぼかしたい、わざとぶらしたいという撮影者の意図を反映させるには操作が必要ですが。
カメラ自身で記録したJPEG
DxOを使って歪曲収差補正を止めるとこのようになります。
ホワイトバランスも調整しましたし、そもそも色が現像ソフトによって若干異なります。
周辺は歪んでいて、カメラ自身が記録したJPEGに写っていない範囲まで写っています。
このように画面の端ほど内側に歪んでいますので、補正するということは外側をさらに外側に引っ張ることになります。
ということは長辺方向をさらに引き延ばしますので、左右の端がはみ出て切り捨てられてしまいます。
DxOで歪曲収差を補正すると、縦横比を保たないことで、はみ出して切り捨てられる部分を減らすことができます。
右端のテレビ局のアンテナを見ると分かりますが、横方向に関しては、最初の、カメラが保存したJPEGより広い範囲が写っています。
縦横比も少し大きくなって、黄金比√5+1:2に近いです。
補正により若干は周辺解像度が下がるはずですが、元々2000万画素なので、普通に見る大きさにリサイズしたらまず分かりません。
最高感度のISO6400で撮ってみました。
ノイズリダクションを切るとざらざらですし、ノイズリダクションをかけると細部が潰れてしまいますが、ブログに載せるために縮小すれば潰れたことは分からなくなります。
少々分厚いとはいえポケットに入る大きさでこの画質は一番だと思います。
これで不満ならポケットには絶対入らないデジカメを用意しなければなりません。
オートフォーカス
他のコンパクトデジカメと比べたら少し速く感じます。しかし位相差AFのNikon1と比べると、Nikon1ならピントが合う筈の被写体で合わないことがあります。
例えば(普通は撮りませんが説明用の例として)青空を背景に電線が一本渡っている場合に、電線にピントを合わせることができませんでした。
電線は撮りませんけど、飛行機雲で困りそうですし、コーヒーカップの中のコーヒーとカップの境界線にも合わせられません。
飛行機雲なら無限遠ですので適当な遠くのものでAFロックかけるという手がありますが、近くのものだと、「Nikon1(に限らず位相差AF)なら簡単に合わせられるのに」と思いながらマニュアルフォーカスすることになります。
そういう場合はRX100に限らずコントラストAFを使うコンデジやミラーレスだとどれも合わないのですが。
また、日暮れ後の風景など、暗くてAF補助光も届かない場合のピンボケ率も高いです。
オートフォーカスくらいはNikon1が勝たないと、RX100と比べて大きい、標準ズームだと暗い、同じ感度で同じ大きさにリサイズするとノイズが多い、ではNikon1の存在意義が危なくなります。
とは言え、ピントが合わなければ、どんなに画素が多くても、ノイズが少なくても意味ないですから、Nikon1の大きさで構わないならNikon1の方が良いと思います。
コントラストAFでもピントを合わせやすいものにピントを合わせる時間を比較して「コントラストAFでも位相差AFと合焦時間がほとんど変わらなくなった」と言われますが、それ以前の問題として、ピントを合わせることが出来る被写体が違いますので、Nikon1にも色々不満はありますが、Nikon1の大きさでも持ち歩ける時はNikon1を使うことになります。
露出プログラム
少しでも暗くなるとすぐ絞りが開放になります。プログラムAEでプログラムシフトを使わないと広角端で1/100 F1.8になりました。
コンデジとしてはセンサーが大きいので、特にマクロだと開放では被写界深度が浅すぎますし、収差も酷くはありませんが少しは絞った方が良いです。
あまり詳しくない人に「予算が許すならこれが一番！」と勧めましたが「全体にピントが合わせられずにボケてしまう」と言われてしまいました。
手振れ補正もありますし高感度ノイズもコンデジとしては少ないので、換算焦点距離分の1までシャッター速度を下げるなりISO400程度まで感度を上げて絞る露出プログラムが良いと思います。
マクロなら特に絞った方が良いと思うのですが、シーンセレクトでマクロを選んでも、感度を上げる前に絞りが開放になります。
結局、絞り優先AEに切り替えて自分で絞るか、感度を手動で上げるか、プログラムシフトを使う必要があり、初心者がカメラ任せでは他のコンデジより綺麗に撮れるとは限りません。
凄く暗いところなら絞り開放しか選択肢がないので、センサーの性能、レンズの明るさという基礎能力で他のコンデジに勝てますが、明るいところだと他のデジカメでは全体にピントが合わせられるのに、この機種でカメラ任せだとピントを合わせた部分以外ボケてしまうことになります。
この点、ニコンの一眼レフのオートモードは、カメラ任せでカメラの画質をほぼ引き出せます。
わざとぼかしたい、わざとぶらしたいという撮影者の意図を反映させるには操作が必要ですが。
絞り、シャッター速度、感度を揃えて他のデジカメと比較すると白飛びしやすいと言われていますが、自動露出だと少し暗めに写す(というか明るい部分を考慮して露出を決めている？)ようで、他のコンデジと比べてむしろ白飛びしにくいと感じます。
暗部ノイズが少ないので、明るい部分が飛ばないようにすることを優先できる余裕があるのでしょう。
画素ピッチから考えるとF2.8から半段絞ったくらいまでが回折の影響を受けないと思います。
広角端は特に写りが良いので周辺まで考えてもF4まで絞れば良いでしょう。ズーム中間域はちょっと苦手なので周辺まで考えて絞ったとしてもF5.6までにとどめた方が良いです。
関係ないですが
google chrome安定版22.0.1229.94
http://cache.pack.google.com/edgedl/chrome/win/22.0.1229.94_chrome_installer.exe
2012-10-11
統計学入門
先週、Excelの入門まで終わらせたので、今日は統計処理の入門として、統計学Iの数値例をExcelで計算します。
例1のデータをエクセルのA列にコピーしてください。
Excelを使って、教科書の例1.2, 例1.4の計算をします。
B2セルの上でマウスの左ボタンを押して、押したままC21セルまでマウスを移動させて左ボタンを離します。
そして画面上の「挿入」から「散布図」の「散布図(マーカーのみ)」を選びます。
すると図のような散布図が得られます。マウスを合わせるとそれが何番目のデータで、x,yの値が何であるか表示されます。
次に回帰直線をExcelに書いてもらいましょう。データ点のどれかにマウスを合わせて右ボタンを押して、表示されるメニューから「近似曲線の追加」を選びます。
「近似または回帰の種類」は「線形近似」を選び、また式も見たいので、「グラフに数式を表示する」にチェックをつけて、閉じるをクリックすると、回帰直線とその式が表示されます。
(y_i-\bar{y})}{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2})
のように陽に書くことが出来ません。Excelを使えばこのような場合も計算できます。
推定値がどれくらいずれているか計算するために、E1セルに「推定誤差」と書いて、E2セルに推定値と実際の座高の差「=D2-C2」を書いて、その式をE21までコピーします。
どのセルをどうしたいのか(最大にする、最小にする)、そのためにどのセルの値を変化させるのか、を尋ねられますので、今回は誤差平方和であるF22を最小にするためにB23からB24までのセルを変化させると入力して「実行」をクリックします。
すると最小にする値を求めてくれます。
準備
左上のファイルからオプションを選びます。
アドインを選んで下の設定を押します。
ソルバーアドインと分析ツールにチェックを付けます。
データ
皆さんが持っている教科書のデータを、一つ一つ入力していると時間がかかりますので、あらかじめ書いておきました。| 例1.1 | 例1.2 | 例1.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
出典 |
ヒストグラム
例1のデータのヒストグラムを書きましょう。例1のデータをエクセルのA列にコピーしてください。
統計学IIの講義で説明するように、95~105, 105~115,...,165~175の区間に分けます。
区間の境界となる105,115,...,165をC列に書きます。
データからデータ分析を選びます。
データ分析からヒストグラムを選びます。
入力範囲欄に観測値を入力したセルを、データ区間欄に区間の境界を書いたセルを指定し、
出力先は少し右隣のE1セルを指定します。
右下のグラフ作成にもチェックを付けてOKを押します。
すると度数分布表とヒストグラムが出来上がります。
このままではx軸の表記がおかしいです。105と書かれた部分は95~105ですし、次の級と書かれた部分は165~175です。そこで各区間の中心値をD列に書いて、これをx軸に使います。
D列のデータをx軸に使うために、グラフを右クリックしてデータの選択を選びます。
右側の横(項目)軸ラベルの編集を押します。
D列に書いた数字を指定します。
これで、横軸に中心値が表示されました。
一種類しかないのに右側に説明がつくのは邪魔ですので消します。
このヒストグラムでは、102と104の人は同じ縦棒に含まれるのに、104の人と106の人は遠くに離れてしまっていますので、棒をくっつけます。
棒の上で右クリックして、データ系列の書式設定を選びます。
要素の間隔をなし(左側)にします。
これで完成です。あとは見やすい大きさに調整してください。
データの特性値
Sheet2に切り替えて、例1.2のデータをA1セルから貼り付けてください。Excelを使って、教科書の例1.2, 例1.4の計算をします。
合計値と代表値を計算します。 B1セルに合計値と書いて、C1セルに =SUM(A1:A30)と書いてください。 B2セルに平均値と書いて、C2セルに =AVERAGE(A1:A30)と書いてください。 B3セルに中央値と書いて、C3セルに =MEDIAN(A1:A30)と書いてください。
次に散布度を計算します。エクセルの参考書で分散を調べるとVARと書かれていますので、
B4セルに分散と書いて、C4セルに =VAR(A1:A30)と書いてください。
すると19.75…と表示されます。
教科書例1.4では19.09となっていますので、計算誤差にしては違いが大きすぎます。
理由は、このVAR関数は不偏分散
を計算しているからです。
これは教科書第4章で、母集団分布の分散を推定するために計算した式です。
教科書第1章では、推定ではなくデータそのものの分散を計算するので
を計算します。
B4セルに先ほど書いた分散を不偏分散に修正して、
B5セルに標本分散と書いて、C5セルに =VARP(A1:A30)と書いてください。
標準偏差も同様に二種類あります。
B6セルに標準偏差と書いて、C6セルに =STDEV(A1:A30)と書いてください。
B7セルに標本標準偏差と書いて、C7セルに =STDEVP(A1:A30)と書いてください。
その他の特性値としては
B8セルに平均偏差と書いて、C7セルに =AVEDEV(A1:A30)と書いてください。
B9セルに最小値と書いて、C7セルに =MIN(A1:A30)と書いてください。
B10セルに最大値と書いて、C7セルに =MAX(A1:A30)と書いてください。
2変量の相関
Sheet3に切り替えて例1.6のデータをA1セルから貼り付けてください。 散布図を描きましょう。B2セルの上でマウスの左ボタンを押して、押したままC21セルまでマウスを移動させて左ボタンを離します。
そして画面上の「挿入」から「散布図」の「散布図(マーカーのみ)」を選びます。
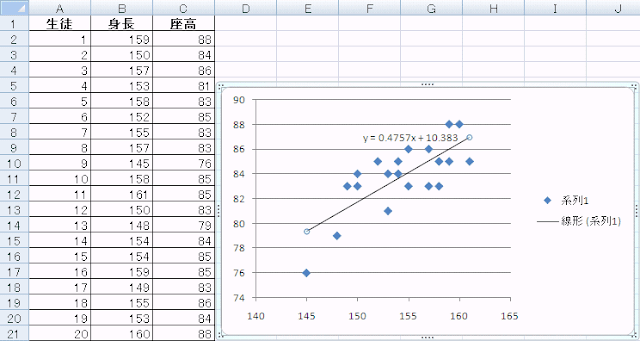
すると図のような散布図が得られます。マウスを合わせるとそれが何番目のデータで、x,yの値が何であるか表示されます。
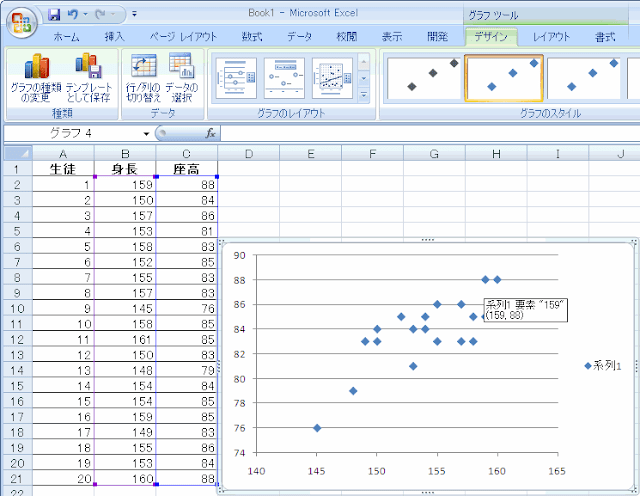
次に回帰直線をExcelに書いてもらいましょう。データ点のどれかにマウスを合わせて右ボタンを押して、表示されるメニューから「近似曲線の追加」を選びます。
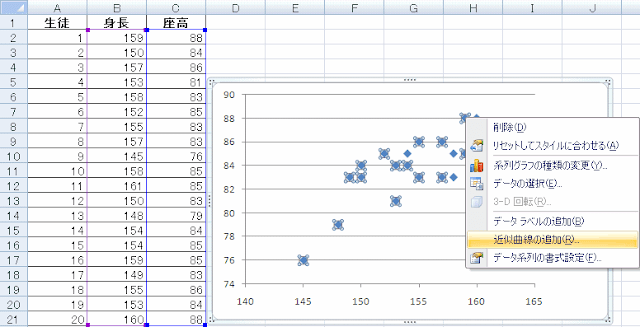
「近似または回帰の種類」は「線形近似」を選び、また式も見たいので、「グラフに数式を表示する」にチェックをつけて、閉じるをクリックすると、回帰直線とその式が表示されます。
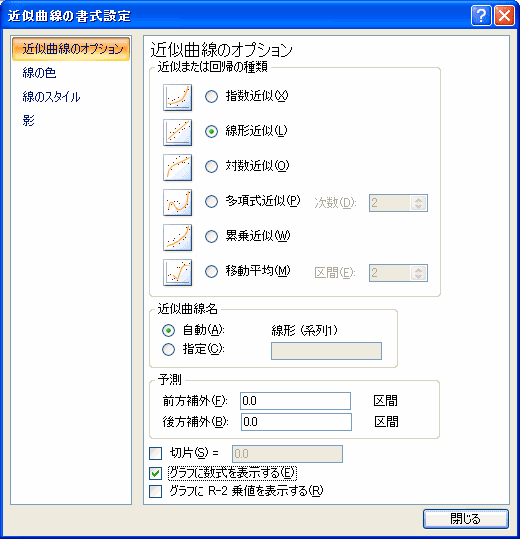
さてこの係数0.4757や定数10.383はどうやって求めましたか？
データを, 直線を
とおくと、
から計算したyの値は
、
これと実際のyの値
との差
を2乗して正の値にしてから足した
を最小にするのでしたね。a,bに関して2次関数で非負ですから必ず最小値を持つので、a,bで偏微分してそれぞれ0とおけばa,bに関する2元連立1次方程式になるのでそれをa,bについて解くことで
と求めることが出来ます。但しはそれぞれ
や
の平均、つまり
です。
ソルバー
もっと複雑な問題を考える時は
座高の推定
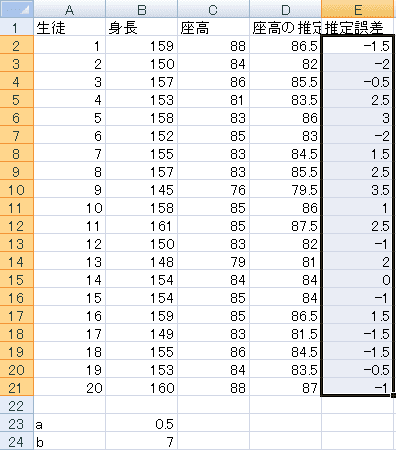
y=ax+bのaとbを、Excelに直接計算させます。そのためにまずaやbの値を書く場所を用意しておきますのでA23セルに「a」、A24セルに「b」と書いてB23セルにaの値、B24セルにbの値を書くことにします。
空っぽだと数字にならないので何か適切な値を書いておきます。全く見当がつかないので、真横の線を書くことにしてaは傾きなので0、bは座高の大体の平均84にしておきます。
このaとbを用いて、y=ax+bという式を用いて身長から座高を推定しますので、D1セルに「座高の推定値」、D2セルに身長とa,bから推定した1番目の生徒の座高の式を書きます。y=ax+bなので「=B23*B2+B24」ですが、D3～D21にコピーしますからa,bを示すB23, B24が変わらないように「=B$23*B2+B$24」と書いておいて、それをコピーします。
当たり前ですが、真横の線で推定したので全て84です。
推定の様子をグラフに書いてみましょう。まず身長、座高、座高の推定値のデータを選択して散布図を描きます。
推定値の方は直線にしたいので推定値の点を右クリックして「データ系列の書式設定」を選びます。
「線の色」は「線(単色)」、「マーカーの種類」は「なし」を選んで「閉じる」をクリックします。
するとグラフがこのようになりますので、B23, B24セルの数字を変化させて直線が点に近付くように調整してみてください。
a=0.5, b=7だとこんな感じです。
あてはまりの良さの評価
見た目で評価したのでは不正確ですので、数値的に評価しましょう。推定値がどれくらいずれているか計算するために、E1セルに「推定誤差」と書いて、E2セルに推定値と実際の座高の差「=D2-C2」を書いて、その式をE21までコピーします。
誤差はプラスにもマイナスにもなるので、そのまま合計、平均を求めると打ち消しあってしまいます。だから二乗してから足し算します。
F1セルに「誤差の二乗」と書いて、F2セルに誤差を二乗した「=E2^2」と書いてF21セルまでコピーします。最後にF22に、その20個の誤差の二乗を合計する式「=SUM(F2:F21)」を書きます。
このF22の値が誤差平方和で、この値が小さいほどあてはまりが良いことになります。この値を小さくするようにa,bの値を調整します。
ソルバーの利用
a,bの値を自分で調整していては大変ですし不正確ですから、Excelに調整させましょう。「データ」を選んで右端の「ソルバー」をクリックします。
どのセルをどうしたいのか(最大にする、最小にする)、そのためにどのセルの値を変化させるのか、を尋ねられますので、今回は誤差平方和であるF22を最小にするためにB23からB24までのセルを変化させると入力して「実行」をクリックします。
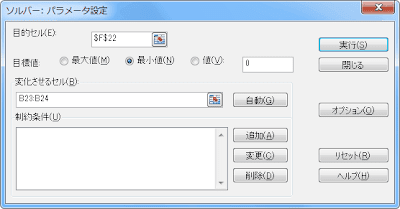
すると最小にする値を求めてくれます。
登録:
投稿 (Atom)
