マクロを使って行列の演算をしてみましょう。
行列の準備
次のように行列を入力してください。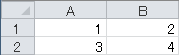
エクセルのワークシートのどの部分が行列なのかを指定します。
Sub gyoretsu()
Dim A As Range
Set A = Range(Cells(1, 1), Cells(2, 2))
最初に、Aはワークシートの範囲を指定するものだと宣言して
次にCells(1, 1)からCells(2, 2)までの長方形が行列Aの範囲だと指定します。
演算してみましょう。
行列一つだけで計算できる例として、転置と、行列式を求めてみます。
Dim B As Range
Set B = Range(Cells(4, 1), Cells(5, 2))
B = Application.Transpose(A)
これで、行列Bの場所であるCells(4, 1)からCells(5, 2)までの長方形に行列Aの転置が出力されます。
Cells(7, 1) = Application.MDeterm(A)
これで、行列Aの行列式がCells(7, 1)に出力されます。
行列の掛け算
今度は二つの行列を掛け算した行列を求めましょう。エクセルのシート1とシート2の両方に先ほどの行列を書いてください。
Sub kakezan()
Dim A As Range, B As Range, C As Range
Set A = Range(Sheets(1).Cells(1, 1), Sheets(1).Cells(2, 2))
Set B = Range(Sheets(2).Cells(1, 1), Sheets(2).Cells(2, 2))
Set C = Range(Sheets(3).Cells(1, 1), Sheets(3).Cells(2, 2))
C = Application.MMult(A, B)
End Sub
これでシート3の行列Cに、行列の積ABが出力されます。
必ず「標準モジュール」にマクロを書いてください。
連立一次方程式
Ax=b
と書けます。
この式に左からAの逆行列を掛けて
x=A-1b
ですから、エクセルを使って計算するのは
Aの逆行列A-1
A-1とbの行列の積
です。
シート1のCells(1, 1)からこの連立一次方程式の係数行列と定数項を並べて
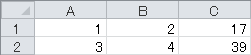
このように代入します。
この中のCells(1, 1)からCells(2, 2)までの長方形を行列A
Cells(1, 3)からCells(2, 3)までの長方形を行列B
シート2のCells(1, 1)からCells(2, 2)までの長方形にAの逆行列を代入するのでここを行列C
シート3のCells(1, 1)からCells(2, 1)までの長方形に、答えの行列行列を代入するのでここを行列D
とします。
Sub renritsu()
Dim A As Range, B As Range, C As Range, D As Range
Set A = Range(Sheets(1).Cells(1, 1), Sheets(1).Cells(2, 2))
Set B = Range(Sheets(1).Cells(1, 3), Sheets(1).Cells(2, 3))
Set C = Range(Sheets(2).Cells(1, 1), Sheets(2).Cells(2, 2))
Set D = Range(Sheets(3).Cells(1, 1), Sheets(3).Cells(2, 1))
C = Application.MInverse(A)
D = Application.MMult(C, B)
End Sub
解けない場合の処理
このような場合に対処するために、逆行列を求める前に行列式を計算して、行列式が0ではない場合だけ連立一次方程式を解くようにしましょう。
場合分けにはIf文を使います。
If 条件 Then
'ここに条件が成立した時に実行する文を書く
Else
'ここに条件が成立しなかった時に実行する文を書く
End If
このように書きます。
条件が成立しなかった時は何も実行しないなら
If 条件 Then
'ここに条件が成立した時に実行する文を書く
End If
練習
ここまでに説明したことを使って、解ける方程式は解く、解けない方程式は「解けません」と表示するマクロを書いてください。解けないと表示するためには
msgbox("解けません")
と書きます。








