2009-06-29

Ask.jp

ZoneAlarmのVista対応版(英語版)を探してきてインストールしようとしたら「スパイウェアをブロックするツールバーもインストールしますか」と尋ねられて「インストールする」を選んだら、ASKツールバーがインストールされました。
どんな会社が作っているのかな？と調べてみたら
プレスリリース：アスクドットジェーピー日本では個人向けサービスは止めるそうです。
Smiley Central スパイウエアについて - スパイウェアガイド
> もし、このウェブサイトやソフトウェアが売却されるような場合、またはウェブサイトやソフトウェアに関わる資産が全面的、部分的にでも譲渡されるような場合には、ユーザから提供された情報や収集された情報はすべて個人情報を含めてサービスの継続のために移管されます。
FunWebProducts (FunWebProducts-AskJeevesJapan)と Ask.jp が配布するツールバー《 futuremix
インストールしない方がよさそうです。

信頼区間

区間推定について説明します。

SILKYPIX

RAW現像ソフトとしてこの方はSILKYPIXを勧めています。
RAW現像ソフトによる色の違い：Komin's Photo Blog：So-net blogとか目がちかちかする芝桜：Komin's Photo Blog：So-net blogなど。
ＨＰ放置日記。 : 有言実行
RAW現像ソフト比較！！　なんてこったい！！ - 金魚ひらひら - Yahoo!ブログ

ディスプレイ（モニター）の調整とカラーマッチング
 ディスプレイガンマの調整
 モニターの色温度調整
 bungen's gallery ～ディスプレイ調整コーナー～

2009-06-26

統計学入門

第一章、第二章の内容のうち、パソコンを使った方が効率的なものについて説明します。
Excelを使ったことが無い人は、総合情報基盤センター利用の手引き第2分冊第三章も読みながらこのホームページを読んで下さい。
下のほうに、オレンジの大きな文字でレポート課題を書いています。

準備

下図のようにメニューを辿ってExcelを立ち上げましょう。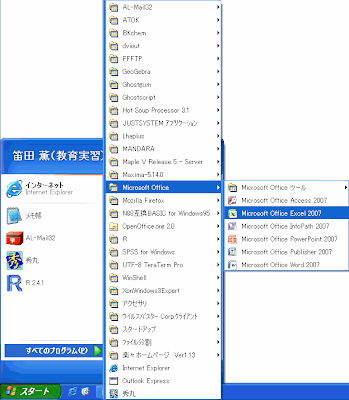

初めて使う時にはいくつか聞かれますので、共にOKを押してください。

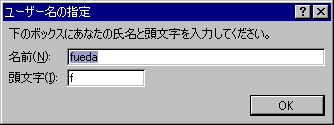
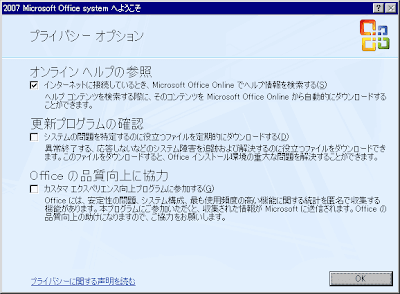
左上の丸いボタンを押して、「Excelのオプション」をクリックします。そして左側の「アドイン」をクリックして、下の「管理:Excelアドイン」の横の「設定」をクリックします。

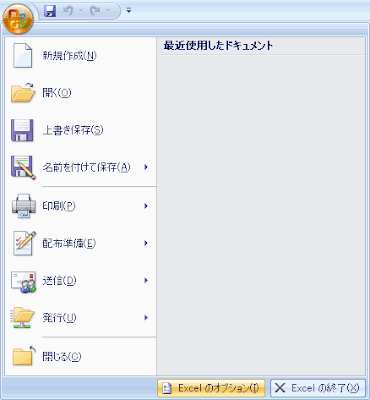
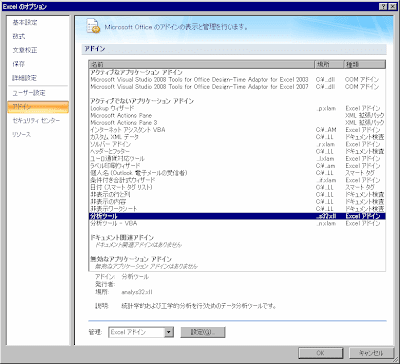
するとアドインの画面に切り替わるので、下のほうの「管理」が「Excelアドイン」になっていることを確かめてその右の「設定」をクリックします。

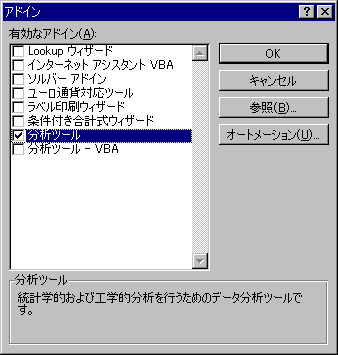
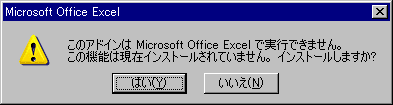
「分析ツール」にチェックをつけてOKをクリックします。「インストールしますか」と聞かれたら「はい」と答えます。

教科書第一章の例

例1.1

例1.2

例1.6

120
106
112
168
120
140
160
160
116
118
104
172
130
124
134
142
112
112
110
120
134
136
138
144
120
120
160
108
140
98
142
130
138
126
108
120
136
118
118
122
128
124
110
134
116
138
116
158
106
166
118
158
124
124
110
166
132
126
122
132

4
5
5
6
6
8
8
8
8
8
9
9
10
10
11
11
11
11
12
12
13
13
15
16
16
16
17
18
20
20

生徒	身長	座高
1	159	88
2	150	84
3	157	86
4	153	81
5	158	83
6	152	85
7	155	83
8	157	83
9	145	76
10	158	85
11	161	85
12	150	83
13	148	79
14	154	84
15	154	85
16	159	85
17	149	83
18	155	86
19	153	84
20	160	88

例1.1　度数分布表とヒストグラム

教科書例1.1のデータをエクセルに入力します。キーボードから入力するか、あるいは上の表をコピーして、エクセルに貼り付けます。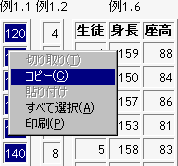

次に、階級の境界の数字をC2セル以降に入力します。

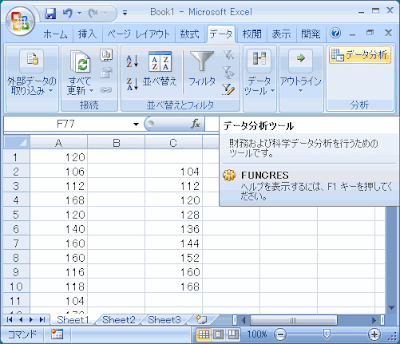
右上の「データ分析」をクリックして「ヒストグラム」をクリックしてOKを押します。

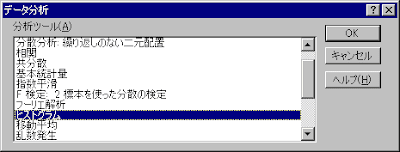
以下のように入力してOKを押します。

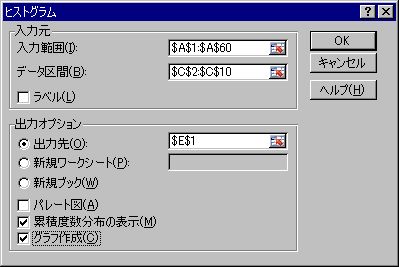
教科書で度数と書かれている部分が、エクセルでは頻度と表示されます。その右には累積相対度数が表示されます。
教科書と同じ結果になりましたか？もし違うなら、その理由を考えてみてください。

例1.2、例1.4　1変量の特性値を求める

エクセル左下のSheet2をクリックして、新しいシートに切り替えます。

そして例1.2のデータをコピーしてA1セルから貼り付けます。A30セルまでデータが30個並んでいるはずです。

まず平均を求めましょう。B1セルに「平均値」と書いてください。
Excelで平均を求める関数はAVERAGEです。C1セルに=AVERAGE(A1:A30)と書いてください。
次に中央値を求めます。B2セルに「中央値」、C2セルに=MEDIAN(A1:A30)を入力します。
次に分散と標準偏差を求めます。まずB3セルに「分散」、B4セルに「標準偏差」と書きます。
第一章では分散を推定するのではなく、単にデータの分散を計算するだけです。このように推定する必要がない場合は分散はVARP、標準偏差はSTDEVPという関数を使いますので、C3セルに=VARP(A1:A30)、C4セルに=STDEVP(A1:A30)と書きます。
ちなみに、推定する場合はVARとSTDEVを使います。

例1.6　2変量の相関を調べる。

エクセル左下のSheet3をクリックして、新しいシートに切り替えて、例1.6のデータをコピーして貼り付けます。
散布図を描きましょう。
B2セルの上でマウスの左ボタンを押して、押したままC21セルまでマウスを移動させて左ボタンを離します。
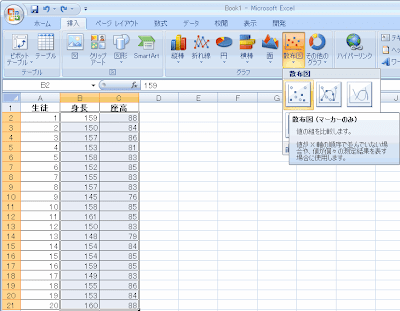
そして画面上の「挿入」から「散布図」の「散布図(マーカーのみ)」を選びます。

すると図のような散布図が得られます。マウスを合わせるとそれが何番目のデータで、x,yの値が何であるか表示されます。

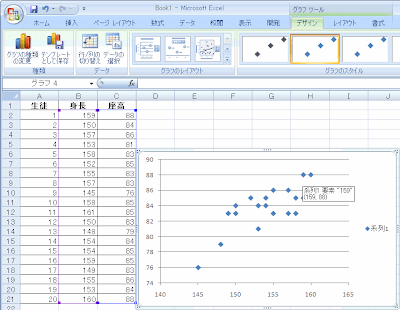
次に回帰直線をExcelに書いてもらいましょう。データ点のどれかにマウスを合わせて右ボタンを押して、表示されるメニューから「近似曲線の追加」を選びます。

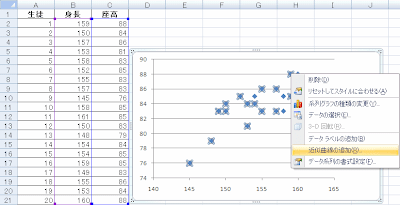
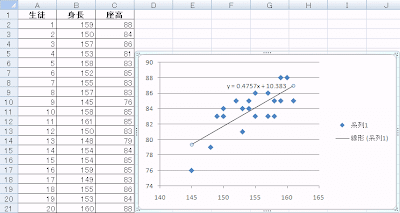
「近似または回帰の種類」は「線形近似」を選び、また式も見たいので、「グラフに数式を表示する」にチェックをつけて、閉じるをクリックすると、回帰直線とその式が表示されます。
「近似または回帰の種類」を変更するといろいろな曲線が表示されます。

第二章:確率関数、分布関数の値の求め方

二項分布B(n,p)の確率関数P(X=x)はエクセルの関数BINOMDIST(x,n,p,FALSE)で求めることが出来ます。
一方分布関数P(X≦x)はBINOMDIST(x,n,p,TRUE)で求めることが出来ます。

まず正しいコインを10回投げたときに、5回表が出る確率を求めてみましょう。
表が出る回数が5回ですのでxは5, 10回投げるのでn=10, 正しいコインなのでp=0.5, 確率関数なので最後は0です。先ほど合計を求めるときに=SUM(A1:A30)と入力したように、どこかのセルに=BINOMDIST(5, 10, 0.5, FALSE)と入力します。
次に6回以上表が出る確率を求めてください。今回は講義中に正解を書けないので数字だけ書いておきます。0.376953…となれば正解、入力した式は正しいです。

しかし、BINOMDISTでは10,000回投げたときに5,000回以上表が出る確率を求めようとしてもnが大きすぎて出来ませんので、こんなときは正規分布で近似します。
正規分布N(μ,σ²)の密度関数f(x)はエクセルの関数NORMDIST(x,μ,σ,FALSE)で求めることが出来ます。
一方分布関数P(X≦x)はNORMDIST(x,μ,σ,TRUE)で求めることが出来ます。

練習:Xの確率分布が標準正規分布の時、P(X≦1)を求めなさい。0.841345…となれば正解です。

次に、二項分布B(n,p)でnが大きいときの正規分布による近似が正しいかどうか確かめるために、BINOMDISTでも計算できるn=100で確かめてみましょう。
正しいコインを100回投げたときに表が出た回数をXとします。
P(X≦50)とP(X≦55)をBINOMDISTを用いて求めてみましょう。それぞれ0.539795…と0.864373…となれば正解です。
Xの分布を正規分布で近似するために期待値μと分散σ²の値を求めてください。公式は教科書にまとめてあります。
P(X≦50)とP(X≦55)を正規分布による近似で求めてください。それぞれ0.5と0.841345…となれば正解です。
少し近似精度が低いですね。講義中に板書した、二項分布の棒グラフと正規分布の密度関数の曲線で囲まれた部分の面積を思い出してください。棒グラフには幅があるので、密度関数を積分するときにもその幅の分だけ広げた方が精度があがります。どのようにすれば精度が上がるか考えてください。0.539828…と0.864334…になります。

レポート課題

正しいさいころを10回転がして出た目の平均が3.9以上になる確率を求めてください。正規分布による近似を使って構いません。
エクセルのNORMDIST関数を使っても構いませんし、講義の手順で求めても構いません。
どのような手順で求めたのかも書いてください。手書きでも、プリントアウトしたものでも構いません。
来週の講義の時間に提出してください。

前回の講義の時に説明した「正しいさいころを10回転がして出た目の平均が3.9以上になる確率」は値が違っていました。
やり方は間違いないのですが、私がエクセルで計算したときに入力し間違えたようで、先週の講義後、暗算で概算したら値がおかしかったので、もう一度エクセルで計算したら別の値になりました。正しい値はレポート課題の解説の時に話します。

発展:二項分布の表

確率関数、分布関数、期待値、分散を公式を使うのではなく定義どおりに求めてみましょう。また先ほどは特定の値にだけ分布関数を求めてみましたが、分布関数全体を求めてみましょう。まず、分布のパラメータを入力します。

xの欄に0から10まで入力します。一つずつ入れていると大変なので、まずA6に0を入れた後は自動で埋めましょう。0を入れたセルをクリックして編集→フィル→連続データの作成を選びます。

列方向に1つずつ10まで増やします。

するとこのようになります。

次に確率関数を入力します。確率関数の式に従ってx=0に対しては
=COMBIN(B$2,A6)*B$3^A6*(1-B$3)^(B$2-A6)
と入力します。

それをB16セルまでコピーして、確率関数の完成です。

次に分布関数を入力します。 x=0に対しては=SUM(B$6:B6)と入力します。

それをC16セルまでコピーします。

次に期待値μ=Σxp(x)を求めます。まずx=0に対して=a6*b6と入力します。

それをD16セルまでコピーします。

それらを合計したものが期待値です。実は期待値はnpとして求めることが出来ます。

次に分散σ^2=Σ(x-μ)^2p(x)を求めます。まずx=0に対して=(a6-d$18)^2*b6と入力します。

それをE16セルまでコピーします。

それらを合計したものが分散です。実は分散はnp(1-p)として求めることが出来ます。

さて、n=10の場合はこのように確率関数、分布関数を計算することが出来ますし、正規近似では近似精度が悪いです。でもnが大きくなると確率関数を計算することが出来なくなる一方、正規近似の精度は良くなります。それで正規分布N(μ,σ²)の分布関数で近似します。とりあえずn=10の場合に対してどれくらい近似できるか見てみましょう。まずx=0に対して
=NORMDIST(a6,d$18,SQRT(e$18),TRUE)と入力します。3番目の引数には分散ではなくその平方根である標準偏差を代入します。

それをF16セルまでコピーします。

さて近似してみましたが、C列とF列を見比べてみると値はかなり異なっています。先ほど書いた、棒グラフの幅が原因です。特にn=10だと棒も11個しかないので、その幅の影響が大きいです。まずx=0に対して
=NORMDIST(a6+0.5,d$18,sqrt(e$18),TRUE)と入力します。つまり幅の分0.5増やしています。

それをG16セルまでコピーします。

如何ですか。小数点以下2桁までは合いました。

2009-06-25

Windows7 RC

試しに入れてみて気づいたことのメモ

マイドキュメント

VISTAまでは、
・マイドキュメントは一箇所
・だから、インストール時と違うところにファイルを置きたいなら「移動」
でした。
ところがWindows7では
・マイドキュメントは何箇所も登録できて、スタートメニューの「ドキュメント」を選ぶとそれらが全部表示される
・保存するときに登録した内のどこに保存するか、は一箇所指定
ということになっています。

SSD

原理的にSSDはデフラグしても有害無益です。VISTAはSSDを特別扱いしないので、普通のハードディスク同様、自動デフラグしていました。Windows7ではSSDもデフラグしようとすれば出来ますが、自動的にデフラグされるスケジュールの対象には出来ません。

一般化情報量規準GIC

最尤推定法に限らず様々な推定法を用いる統計モデルを評価するために、一般化情報量規準GICと、それを理解するために必要な統計的汎関数について説明します。

2009-06-22

カスタムピクチャーコントロール

ニコンのピクチャーコントロールは、他の人が作ったものをデジカメ本体やCaptureNX2などのソフトに登録することが出来ます。
但し、他社カメラに乱用されないためなのかどうか目的は分かりませんが、単純にコピーしただけでは認識されません。恐らくニコンのデジカメでSDカードやCFカードをフォーマットしたときに作られる隠し属性ファイルに何か書き込んでいるのでしょう。

従って次の手順が必要です。
まずSDカードやCFカードをピクチャーコントロールに対応したデジカメでフォーマットします。デジカメ本体に登録するなら、登録したいデジカメ自身でフォーマットします。ソフトに登録するなら、カメラはピクチャーコントロールに対応していればどれでも構いません。
フォーマットしたカードをパソコンのカードリーダーに入れて、ViewNXやCaptureNX2のPicture Control Utilityを起動します。そして元々入っているピクチャーコントロールのどれかを適当に変更してカードに保存します。するとカードにNIKONというフォルダと、その中にCUSTOMPCというフォルダが作られますので、CUSTOMPCフォルダの中に他所で作られたピクチャーコントロールのファイルをコピーします。
もう一度Picture Control Utilityに戻って、インポートを押すと、コピーしたファイルが見えますのでそれを開いて、改めて同じカードに保存しなおします。
そのカードを、フォーマットしたカメラに入れて、メモリカードから登録を選ぶと、コピーしたピクチャーコントロールが選択肢に表示されます。

\NIKON\CUSTOMPCフォルダを自分で作ると駄目なようです。あくまでPicture Control Utilityに作らせる必要があります。

中心極限定理

中心極限定理とその応用を説明し、ガンマ関数、ベータ関数、χ²分布、t分布、F分布を紹介します。

2009-06-19

中心極限定理

中心極限定理とその応用を説明し、ガンマ関数、ベータ関数、χ²分布、t分布、F分布を紹介します。

2009-06-18

一般化線形モデル

様々な問題に対してどのようにして統計モデルを構築する方法として、一般化線形モデルと、そのために必要な指数型分布族について説明します。

2009-06-17

D90

使っているうちに気づいたことを書いていこうと思います。

ファインダー: やはりペンタプリズムは見易いです。受光素子はD5000と同じなのですが、ファインダーの見易さが違います。
露出制御: D60同様、ニコンの3D-RGBマルチパターン測光IIは暗い部分、特に画面中央(正確に言うとオートフォーカスがピントを合わせようとした部分)が暗くならないように、明るめに写します。それを防ぐためにD60の時にはマイナスの露出補正をかけていました。でもこれだと、中央部重点測光を使うときに露出補正を戻し忘れることがありました。
D90だと基準露出レベルを測光方式別に設定できますから、マルチパターン測光だけマイナスにしています。
このままだと写真が少し暗めになります。RAWファイルを後でパソコンで処理する場合はその時に調整できますが、その作業を省いて、同時に記録されるJPEGをそのまま使うときは暗いままです。そこでピクチャーコントロールの明るさを＋１にしています。
アクティブD-ライティング: 以前書いたように写真全体として不自然に感じることがあるので、私は使わないことにしています。撮影するときは使っておいて、RAWファイルを処理するときに解除することも出来ますし、そうすれば同時記録のJPEGだけアクティブD-ライティングを使うことも出来ます。但しアクティブD-ライティングを使うとピクチャーコントロールの明るさもアクティブD-ライティング任せになって自分で設定できません。
アクティブD-ライティングは、強度に応じて撮影時に露出を暗くし、その分現像時に明るくします。オートにして撮影してオフで現像すると、明暗差に応じたマイナス露出補正として使うことが出来ます。
オートフォーカス: D60同様速くて正確です。でも3Dトラッキングを使うには11点では足りないと感じます。オートエリアは飛ぶ鳥を撮影するような、動きを追えない時には便利ですが、時間があるときならシングルポイントで自分で指定した方が良いですので、Fnボタンの機能をAFエリアモード設定にしておいて
・通常はオートエリアにして、急な機会に備える
・時間があるときはシングルポイントに切り替えて自分で合わせる
・シングルポイントのために、OKボタンの機能を「フォーカスポイント中央リセット」に設定する
にしています。
ライブビューでは、位相差AFが使えず、コントラストAFだけです。正直言って遅くて不正確で使う気になりません。まずファインダーを見てピントを合わせてからマニュアルフォーカスに切り替えてライブビューでなければ写せないアングルから写す、という使い方になりそうです。
D300のように位相差AFも使えると便利です。Carl Zeissのような、明るくて被写界深度が浅いマニュアルフォーカスレンズでじっくりとピントを合わせる時には便利だと思います。
ホワイトバランス: B2M0にしています。もう少し紫が欲しいのですが、B2M1だと顔が紫色になります。
ノイズ: ニコンの最近のCMOSは塗りつぶしているからノイズが少なく見えるだけという見方もありますが、D60よりS/N比は良いです。D60で同じくらいノイズを減らそうとするともっとボケます。元々ノイズが少ないので、高感度ノイズリダクションはオフにしています。長時間ノイズリダクションの方は、後処理では利用できない情報を活かしていますのでオンにしています。
ワタシがいかにして...は結構あちこちで引用されていますが、EOS DIGITAL 掲示板のm2nさんの書き込みが参考になりました。
D700はノイズが少ないのでバンディングが目立つようです
インターバルタイマー: 価格.com - 『無線式シャッターレリーズ』ニコン D90 のクチコミ掲示板によると、MC-36とMC-DC2を買ってきて
> 基板のムラサキに白線、シロに緑線、クロにシールド、キイロに黒線、ミドリは空
だそうです。

全体的にD60よりいろんな面で優れているけれど、それに相当するくらい高くて重くいので、どちらが一方的に良い、ということはないと感じます。
D60は495g、キットレンズの18-55VRは265g、一方D90は620g、私はそれに16-85をつけていてこれが485gですから、合計で760g対1105gで、持った感じがだいぶ違います。というかこの重さのおかげでD300の長所を見ても我慢できます(笑)
というかボディの差が125gに対してレンズの差が220gもあるのか…
ちなみにD700にAF Nikkor 35mmF2Dを付けると995+205=1200gで単焦点なのにもっと重くなります。

後藤哲朗氏本人に訊く：ニコンが設立した「後藤研究室」とは - デジカメWatch
> 実はニコンの一眼レフで、もっとも完成された自動機能が搭載され、簡単に思い通りの写真が撮れるのはD3シリーズなどの上位機種だと思います。D3で写真を撮影することに比べると、D40は難しいとも言えます」
> －－D3/D300は露出判別やオートフォーカス、ストロボ調光など、実に的確な判断をしてくれて、ほかのカメラと使い比べると露出補正が必要になる場面が少なくて驚きます。しかし、同様のアプローチで露出制御しているD90には（測光センサーの違いもあって）、あそこまでの素晴らしさはない。D40になると普通の一眼レフカメラになってくる。レリーズレスポンスやファインダー消失時間といった要素も含めると、確かにD3/D300というのは実にイージーなカメラですね。

2009-06-15

標本分布

標本分布や、定理2.4で出てきた確率変数の独立性について説明します。教科書84ページの定理3.1は重要です。

2009-06-13

岡山県総合グラウンド

道端に立派な花が咲いていました。

グラウンドを一周していたら、日が沈んで暗くなりました。

翌日は晴れて綺麗な夕日が見られました。

一人っ子。巣が小さいようです。来年は大きな家に引っ越してください。

ピンボケ。後ろの葉っぱにピントが合ってしまいました。

2009-06-12

標本分布

標本分布や、定理2.4で出てきた確率変数の独立性について説明します。教科書84ページの定理3.1は重要です。

2009-06-11

最尤推定法

先週の練習問題の注意点

σ^2の値をパラメータにすると、ソルバーが負の数を代入するとエラーになります。範囲に制限をつけても良いのですが、簡単にするために、σの値をパラメータにします。するとソルバーが負の値を代入しても、2乗して正の数になるので大丈夫です。
Excelで -A1^2 と書くと(-A1)*(-A1)の意味になります。-A1*A1の意味にするには -(A1^2) と書いてください。
A1/B1*C1 と書くと、A1をB1で割ってC1を掛けることになります。B1*C1でA1を割るには A1/(B1*C1) と書いてください。
パラメータの値として最初に代入する値があまりにもデータと離れすぎていると、尤度が殆ど0になって対数尤度がマイナス無限大になってしまいます。先週の記事のデータの最後に平均と標準偏差を追加で書いておきました。初期値として水平な線を当てはめることを考えて、αには平均値に近い値として3000, βは水平なので0, σは標準偏差に近い値として270を最初に代入してください。

モデル1の最尤推定量を求めるとこのようになります。

レポート課題1

次の3つのモデルの中から、AICを用いて最も適切なモデルを選びなさい。

モデル1: 体重の分布は男女とも正規分布N(α+βx,σ²)である。
モデル2: 男の子の体重の分布は正規分布N(α₁+βx,σ²), 女の子の体重は正規分布N(α₂+βx,σ²)である。βとσは男女共通で、切片αだけ異なる。
モデル3: 男の子の体重の分布は正規分布N(α₁+β₁x,σ²), 女の子の体重は正規分布N(α₂+β₂x,σ²)である。σは男女共通で、切片αと傾きβが異なる。

解答例(わざと見辛くしています。自分で計算してください。)

教科書のデータ

表6.3 20名の男性インスリン依存性糖尿病患者の
炭水化物摂取量, 年齢,
身長から計算された理想体重に対する実際の体重の比率%,
蛋白摂取量

表7.2 かぶと虫の死亡データ
ガス濃度はlog₁₀CS₂mgl^-1

炭水化物	年齢	体重	蛋白
y	x₁	x₂	x₃
33	33	100	14
40	47	92	15
37	49	135	18
27	35	144	12
30	46	140	15
43	52	101	15
34	62	95	14
48	23	101	17
30	32	98	15
38	42	105	14
50	31	108	17
51	61	85	19
30	63	130	19
36	40	127	20
41	50	109	15
42	64	107	16
46	56	117	18
24	61	100	13
35	48	118	18
37	28	102	14

ガス濃度	かぶと虫の数	死亡数
x	n	y
1.6907	59	6
1.7242	60	13
1.7552	62	18
1.7842	56	28
1.8113	63	52
1.8369	59	53
1.861	62	61
1.8839	60	60

出典

レポート課題2

表6.3の炭水化物Yの分布として次の8つのモデルを考えて、AICを用いて選択しなさい。

正規分布N(β₀+β₁x₁+β₂x₂+β₃x₃,σ²)
正規分布N(β₀+β₁x₁+β₂x₂,σ²)
正規分布N(β₀+β₁x₁+β₃x₃,σ²)
正規分布N(β₀+β₂x₂+β₃x₃,σ²)
正規分布N(β₀+β₁x₁,σ²)
正規分布N(β₀+β₂x₂,σ²)
正規分布N(β₀+β₃x₃,σ²)
正規分布N(β₀,σ²)

ロジスティック回帰

表7.2から、ガス濃度毎の死亡割合を計算して図にしました。

このデータに基づいて、死亡確率をガス濃度の関数として表したいと思います。但し確率は0から1の間ですので、直線や多項式を用いると、ガス濃度によっては0から1の範囲をはみ出てしまうので不適です。そこで0から1の範囲をはみ出さないモデルとして次の3つがしばしば使われます。
表の上からi番目の行は、ガス濃度がx_iであるときに、かぶと虫n_i匹の中のx_i匹が死んだということを表しますので、各々のかぶと虫に関して死んだら1、生き残ったら0となるデータをn_i個観測したら、x_i個が1だった、ということになります。従って二項分布B(1,p_i)に従う確率変数をn_i個観測したと考えて、このp_iをx_iのどのような関数で表すか、という問題になります。二項分布の確率関数p(x)=_nC_xp^x(1-p)^n-xで、Excelでは_nC_x=COMBIN(n,x)ですが、₁C₀も₁C₁も1なので省いて構いません。

モデル1:ロジスティックモデル: 死亡数の分布は二項分布B(n_i, exp(α+βx_i)/(1+exp(α+βx_i)))である。
モデル2:プロビットモデル: 死亡数の分布は二項分布B(n_i, Φ((x_i-μ)/σ))である。但しΦは標準正規分布の分布関数で、Excelでは Φ((x-μ)/σ))=NORMDIST(x,μ,σ,1)で書けます。
モデル3:極値モデル: 死亡数の分布は二項分布B(n_i, 1-exp(-exp(α+βx_i))である。

まずロジスティックモデルで確率を計算しましょう。

次に対数尤度の計算です。確率関数はp^x(1-p)^n-xでしたから、x=1ならば尤度はp、x=0ならば尤度は1-pです。x=1がx_i個、x=0がn_i-x_i個ですので、対数尤度はx_ilog p_i+(n_i-x_i)log (1-p_i)をiを1から8まで全部足したものになります。

F12セルの対数尤度を最大にするようなF1、F2セルの値を、ソルバーを用いて求めてください。
モデルによって推定した死亡確率と、実際の死亡割合を比較するとこのようになります。

点は実際の死亡割合、曲線がモデルです。

プロビットモデルに関しても同様にまず確率を求めて、それから対数尤度を計算してみましょう。μは最初はデータの中ごろということで1.8、σはとりあえず1にしてソルバーを使ってください。

すると、分母のσが0になってエラーになりました。
0にならないように変数の範囲に制約をつけましょう。

制約条件(U)の追加(A)をクリックします。

制約をつけるセルはH2、制約式に＞0 と書きたいのですが、≧しか使えないのでとりあえず ≧0.1 と書きます。
OKをクリックすると思いがちですが、何故か追加(A)、キャンセルの順番でクリックしないと怒られます。

制約条件が追加されているのを確認したら実行します。

すると最適化は実行されましたが、σの値が先ほど書いた制約式の端っこである0.1になっています。
制約を変えると最適値も変わるかも知れません。

制約式を変えるために、先ほどの制約式をクリックして変更(C)をクリックします。
制約条件の0.1を0.01に書き換えて、先ほど同様追加(A)とキャンセルをクリックして、制約式が変わっているのを確かめてから実行します。

すると0.01では小さすぎてエラーになりました。

仕方ないので、今度は0.02にして実行してみましょう。

すると制約式の端っこではない最適値が求まりました。