Excelを使ったことが無い人は、総合情報基盤センター利用の手引き第2分冊第三章も読みながらこのホームページを読んで下さい。
下のほうに、オレンジの大きな文字でレポート課題を書いています。
準備
下図のようにメニューを辿ってExcelを立ち上げましょう。
初めて使う時にはいくつか聞かれますので、共にOKを押してください。
左上の丸いボタンを押して、「Excelのオプション」をクリックします。そして左側の「アドイン」をクリックして、下の「管理:Excelアドイン」の横の「設定」をクリックします。
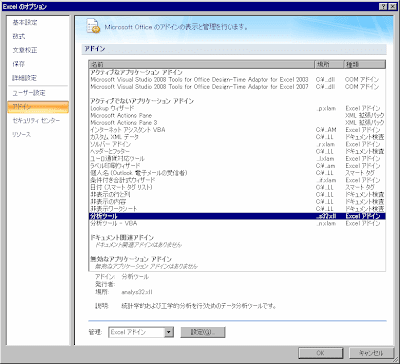
するとアドインの画面に切り替わるので、下のほうの「管理」が「Excelアドイン」になっていることを確かめてその右の「設定」をクリックします。
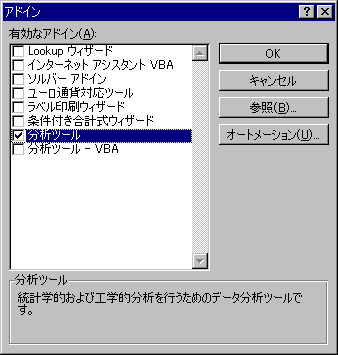
「分析ツール」にチェックをつけてOKをクリックします。
「インストールしますか」と聞かれたら「はい」と答えます。
教科書第一章の例
| 例1.1 | 例1.2 | 例1.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
例1.1 度数分布表とヒストグラム
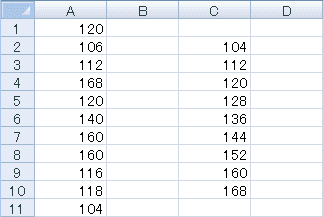
教科書例1.1のデータをエクセルに入力します。キーボードから入力するか、あるいは上の表をコピーして、エクセルに貼り付けます。
次に、階級の境界の数字をC2セル以降に入力します。
右上の「データ分析」をクリックして「ヒストグラム」をクリックしてOKを押します。
以下のように入力してOKを押します。
教科書で度数と書かれている部分が、エクセルでは頻度と表示されます。その右には累積相対度数が表示されます。
教科書と同じ結果になりましたか?もし違うなら、その理由を考えてみてください。
例1.2、例1.4 1変量の特性値を求める
エクセル左下のSheet2をクリックして、新しいシートに切り替えます。
そして例1.2のデータをコピーしてA1セルから貼り付けます。A30セルまでデータが30個並んでいるはずです。
まず平均を求めましょう。B1セルに「平均値」と書いてください。
Excelで平均を求める関数はAVERAGEです。C1セルに=AVERAGE(A1:A30)と書いてください。
次に中央値を求めます。B2セルに「中央値」、C2セルに=MEDIAN(A1:A30)を入力します。
次に分散と標準偏差を求めます。まずB3セルに「分散」、B4セルに「標準偏差」と書きます。
第一章では分散を推定するのではなく、単にデータの分散を計算するだけです。このように推定する必要がない場合は分散はVARP、標準偏差はSTDEVPという関数を使いますので、C3セルに=VARP(A1:A30)、C4セルに=STDEVP(A1:A30)と書きます。
ちなみに、推定する場合はVARとSTDEVを使います。
例1.6 2変量の相関を調べる。
エクセル左下のSheet3をクリックして、新しいシートに切り替えて、例1.6のデータをコピーして貼り付けます。散布図を描きましょう。
B2セルの上でマウスの左ボタンを押して、押したままC21セルまでマウスを移動させて左ボタンを離します。
そして画面上の「挿入」から「散布図」の「散布図(マーカーのみ)」を選びます。
すると図のような散布図が得られます。マウスを合わせるとそれが何番目のデータで、x,yの値が何であるか表示されます。
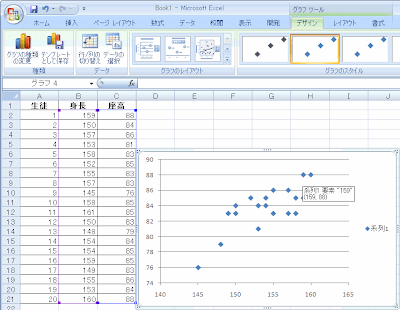
次に回帰直線をExcelに書いてもらいましょう。データ点のどれかにマウスを合わせて右ボタンを押して、表示されるメニューから「近似曲線の追加」を選びます。
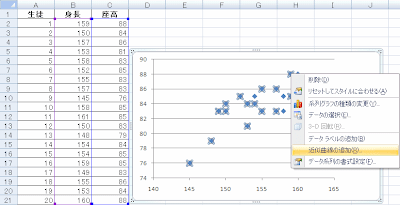
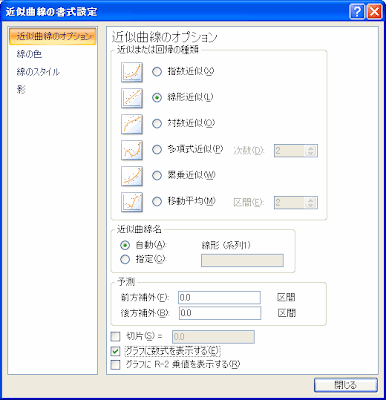
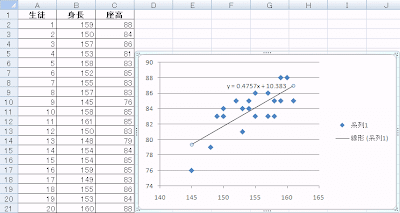
「近似または回帰の種類」は「線形近似」を選び、また式も見たいので、「グラフに数式を表示する」にチェックをつけて、閉じるをクリックすると、回帰直線とその式が表示されます。
「近似または回帰の種類」を変更するといろいろな曲線が表示されます。
第二章:確率関数、分布関数の値の求め方
二項分布B(n,p)の確率関数P(X=x)はエクセルの関数BINOMDIST(x,n,p,FALSE)で求めることが出来ます。一方分布関数P(X≦x)はBINOMDIST(x,n,p,TRUE)で求めることが出来ます。
まず正しいコインを10回投げたときに、5回表が出る確率を求めてみましょう。
表が出る回数が5回ですのでxは5, 10回投げるのでn=10, 正しいコインなのでp=0.5, 確率関数なので最後は0です。
先ほど合計を求めるときに=SUM(A1:A30)と入力したように、どこかのセルに=BINOMDIST(5, 10, 0.5, FALSE)と入力します。
次に6回以上表が出る確率を求めてください。今回は講義中に正解を書けないので数字だけ書いておきます。0.376953…となれば正解、入力した式は正しいです。
しかし、BINOMDISTでは10,000回投げたときに5,000回以上表が出る確率を求めようとしてもnが大きすぎて出来ませんので、こんなときは正規分布で近似します。
正規分布N(μ,σ2)の密度関数f(x)はエクセルの関数NORMDIST(x,μ,σ,FALSE)で求めることが出来ます。
一方分布関数P(X≦x)はNORMDIST(x,μ,σ,TRUE)で求めることが出来ます。
練習:Xの確率分布が標準正規分布の時、P(X≦1)を求めなさい。0.841345…となれば正解です。
次に、二項分布B(n,p)でnが大きいときの正規分布による近似が正しいかどうか確かめるために、BINOMDISTでも計算できるn=100で確かめてみましょう。
正しいコインを100回投げたときに表が出た回数をXとします。
P(X≦50)とP(X≦55)をBINOMDISTを用いて求めてみましょう。それぞれ0.539795…と0.864373…となれば正解です。
Xの分布を正規分布で近似するために期待値μと分散σ2の値を求めてください。公式は教科書にまとめてあります。
P(X≦50)とP(X≦55)を正規分布による近似で求めてください。それぞれ0.5と0.841345…となれば正解です。
少し近似精度が低いですね。講義中に板書した、二項分布の棒グラフと正規分布の密度関数の曲線で囲まれた部分の面積を思い出してください。棒グラフには幅があるので、密度関数を積分するときにもその幅の分だけ広げた方が精度があがります。どのようにすれば精度が上がるか考えてください。0.539828…と0.864334…になります。
レポート課題
正しいさいころを10回転がして出た目の平均が3.9以上になる確率を求めてください。正規分布による近似を使って構いません。エクセルのNORMDIST関数を使っても構いませんし、講義の手順で求めても構いません。
どのような手順で求めたのかも書いてください。手書きでも、プリントアウトしたものでも構いません。
来週の講義の時間に提出してください。
前回の講義の時に説明した「正しいさいころを10回転がして出た目の平均が3.9以上になる確率」は値が違っていました。
やり方は間違いないのですが、私がエクセルで計算したときに入力し間違えたようで、先週の講義後、暗算で概算したら値がおかしかったので、もう一度エクセルで計算したら別の値になりました。正しい値はレポート課題の解説の時に話します。
発展:二項分布の表
確率関数、分布関数、期待値、分散を公式を使うのではなく定義どおりに求めてみましょう。また先ほどは特定の値にだけ分布関数を求めてみましたが、分布関数全体を求めてみましょう。 まず、分布のパラメータを入力します。xの欄に0から10まで入力します。一つずつ入れていると大変なので、 まずA6に0を入れた後は自動で埋めましょう。0を入れたセルをクリックして 編集→フィル→連続データの作成を選びます。
列方向に1つずつ10まで増やします。
するとこのようになります。
次に確率関数を入力します。確率関数の式に従ってx=0に対しては
=COMBIN(B$2,A6)*B$3^A6*(1-B$3)^(B$2-A6)
と入力します。
それをB16セルまでコピーして、確率関数の完成です。
次に分布関数を入力します。 x=0に対しては=SUM(B$6:B6)と入力します。
それをC16セルまでコピーします。
次に期待値μ=Σxp(x)を求めます。まずx=0に対して=a6*b6と入力します。
それをD16セルまでコピーします。
それらを合計したものが期待値です。実は期待値はnpとして求めることが出来ます。
次に分散σ^2=Σ(x-μ)^2p(x)を求めます。まずx=0に対して=(a6-d$18)^2*b6と入力します。
それをE16セルまでコピーします。
それらを合計したものが分散です。実は分散はnp(1-p)として求めることが出来ます。
さて、n=10の場合はこのように確率関数、分布関数を計算することが出来ますし、正規近似では近似精度が悪いです。でもnが大きくなると確率関数を計算することが出来なくなる一方、正規近似の精度は良くなります。それで正規分布N(μ,σ2)の分布関数で近似します。
とりあえずn=10の場合に対してどれくらい近似できるか見てみましょう。
まずx=0に対して
=NORMDIST(a6,d$18,SQRT(e$18),TRUE)と入力します。3番目の引数には分散ではなく
その平方根である標準偏差を代入します。
それをF16セルまでコピーします。
さて近似してみましたが、C列とF列を見比べてみると値はかなり異なっています。
先ほど書いた、棒グラフの幅が原因です。特にn=10だと棒も11個しかないので、その幅の影響が大きいです。
まずx=0に対して
=NORMDIST(a6+0.5,d$18,sqrt(e$18),TRUE)と入力します。つまり幅の分0.5増やしています。
それをG16セルまでコピーします。
如何ですか。小数点以下2桁までは合いました。








0 件のコメント:
コメントを投稿