ブートストラップ情報量規準EIC

前回のロジスティック回帰では、3つのモデルともパラメーターの個数は同じですのでAICによる比較では単純に対数尤度が大きいモデルが選ばれてしまいますし、そもそも3つのモデルは全部異なる関数形ですので、3つ全てが真の分布を含む、つまりAICの条件を満たすことはありません。
そこでEICによるバイアスの導出を行いますが、前回のロジスティック回帰における最尤推定量の計算がまだの人はそちらを先にやってください。

VBAの準備

EICの計算のために用いるブートストラップ法は、乱数を沢山発生させて繰り返し計算しますので、プログラミングが必要となります。

まず準備です。左上の丸いボタンを押して、「Excelのオプション」をクリックします。そして「[開発]タブをリボンに表示する」にチェックをつけてOKを押します。

すると右端に「開発」が表示されるのでクリックして、マクロのセキュリティをクリックして、「すべてのマクロを有効にする」に●をつけてOKを押します。


これで準備は完了です。
ではマクロでどんなことが出来るか見てみましょう。「マクロの記録」をクリックしてください。マクロの名前を聞かれますので、ここはそのままOKを押します。


何か適当にExcelの操作をしてください。ここでは1から5の数字を入力してみました。
そして、記録終了をクリックしてください。

すると、Excelは今の操作を全部覚えています。確かめるために、今入力したものを全部消してから、今度は「マクロ」をクリックしてください。するとどのマクロを実行するか聞かれます。今は一つしかないのでそのまま「実行」を押します。
すると、先ほど自分でやったことがそのまま繰り返されたはずです。


一体どんな仕組みになっているか見るために「Visual Basic」のボタンを押します。するとVisual Basicの画面が開くので、左側のModule1をダブルクリックするとこの画面になります。


先ほど「マクロの記録」をクリックしてから「記録終了」をクリックするまでの操作が全てプログラムに書かれたのです。今すぐ覚える必要はありませんが、ActiveCell.FormulaR1C1 = "1"は選択しているセルに1を代入しなさい、Range("A2").SelectはA2セルを選択しなさい、という命令です。
このように自分の操作をプログラムに記録するのではなくて、今度は自分でプログラムを書いてみましょう。今、人によって色々違うことを書いたと思うので、一旦Excelを終了させて、もう一度立ち上げて、先ほど同様「開発」をクリックして「Visual Basic」をクリックしてください。
プログラムを書く部分を用意したいので「挿入」をクリックして「標準モジュール」をクリックしてください。

現れた画面にプログラムを書きます。
まず
sub 練習
とだけ書いて、Enterキーを押してください。すると自動的に

Sub 練習()

End Sub

となり、カーソルは真ん中の空行にあります。そこに
cells(1,1)=1
と書いてください。これは上から1番目、左から1番目のセルに1を代入しなさい、という命令です。
プログラムを書いたら、上の右向きの三角をクリックしてください。するとさっきと同じように、どのプログラムを実行するか聞かれます。今は一つしか書いていないのでそのまま実行を押すと、A1セルに1が代入されます。Excelの画面で「マクロ」を押しても実行できます。

このプログラムを保存する時の注意。
左上の「上書き保存」を押すと、どの形式でファイルを保存するか尋ねられます。ファイルの種類として「Excelマクロ有効ブック」を指定してください。

さてこれでプログラムを書いて実行できるようになったので、具体的なプログラミングを始めましょう。
先ほどのCells(1,1)=1とEnd Subの間に
cells(2,1)=2
cells(3,1)=3
と書き込んで実行してみてください。
あるいは
cells(1,2)=-2
cells(1,3)=-3
と書いて、cellsの二つの添え字がExcelのどのセルに対応しているか確認しましょう。

10個続けて書くには、
cells(1,1)=1
cells(2,1)=2
cells(3,1)=3
cells(4,1)=4
cells(5,1)=5
cells(6,1)=6
cells(7,1)=7
cells(8,1)=8
cells(9,1)=9
cells(10,1)=10

と書くのは大変なので、これをFor文を使って

for i=1 to 10
　cells(i,1)=i
next　i

と書きます。

練習として下のような九九の表ができるようにプログラムを考えて見ましょう。

ブートストラップ法

前回のロジスティック回帰の続きに書きましょう。

G列にブートストラップ標本を入力することにしましょう。最初のガス濃度が1.6907の行は、59匹中死んだのが6匹ですから、ブートストラップ標本は6個の1と53個の0の中から、毎回戻しながら59回ランダムに取り出すことで得られます。毎回、1を取り出す確率は6/59ですので、1になる確率が6/59で0になる確率が53/59である乱数を59個足せば良いことになります。VBAでrnd()は0から1の一様乱数ですのでrnd()<6/59である確率が丁度6/59です。よって
wa=0
for k=1 to 59
　if rnd()< cells(4,3)/cells(4,2) then
　　wa=wa+1
　end if
next k
cells(4,7)=wa
と書くと、G4セルにブートストラップ標本が抽出できます。
これを第4行から第11行まで繰り返すので、上のプログラムを別のFor文で繰り返して for j=4 to 11
　wa=0
　for k=1 to cells(j,2)
　　if rnd()< cells(j,3)/cells(j,2) then
　　　wa=wa+1
　　end if
　next k
　cells(j,7)=wa
next j
によって全てのガス濃度レベルに対してブートストラップ標本が抽出できました。

この標本に対して改めてパラメータを求めるのでI1,I2セルにとりあえず元々の標本用のパラメータを書いて、後で最尤法で最適値を求めることにします。このα、βを用いて前回同様確率と対数尤度を求めます。
乱数を使っていますので、値が少々違っても気にしなくて構いません。

そしてソルバーを使ってα、βの最適値を求めますが、これを後で繰り返しますので「新しいマクロの記録」を使ってVBAに記録しておきます。
SolverOk SetCell:="$I$12", MaxMinVal:=1, ValueOf:="0", ByChange:="$I$1:$I$2"
SolverSolve
このように記録された筈ですが、このままでは実行できません。
SOLVER.XLAへの参照設定が必要ですのでツールの参照設定をクリックします。

そこにSOLVER.XLAがあればよいのですが、無いので参照をクリックします。

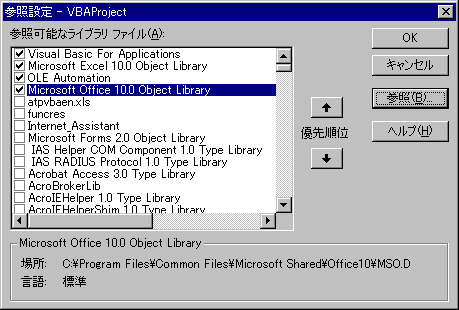
C:\Program Files\Microsoft Office\Office(バージョンによって違う数字)\Library\Solverを指定してファイルの種類をMicrosoft Excel Files (*.xls;*.xla)を選びます。

すると参照設定の一覧の中にSOLVER.XLAが現れてチェックされているのでOKを押します。

このまま実行すると

このようなエラーが出ることがあります。Officeのバージョンによっては出ないこともあるようです。このエラーが出たときには
SolverOk SetCell:="$I$12", MaxMinVal:=1, ValueOf:="0", ByChange:="$I$1:$I$2"
SolverSolve
の直前に
Application.Run "Solver.xla!Auto_Open"
と書くと出なくなります。
またソルバーが終了するたびに確認を求められたのでは自動的に繰り返せないので
SolverSolve
を
SolverSolve Userfinish:=True
に書き直します。

ここまでを実行してみましょう。
For j = 4 To 11
　wa = 0
　For k = 1 To Cells(j, 2)
　　If Rnd() < Cells(j, 3) / Cells(j, 2) Then
　　　wa = wa + 1
　　End If
　Next k
　Cells(j, 7) = wa
Next j
Application.Run "Solver.xla!Auto_Open"
SolverOk SetCell:="$I$12", MaxMinVal:=1, ValueOf:="0", ByChange:="$I$1:$I$2"
SolverSolve Userfinish:=True
ブートストラップ標本を抽出して最尤法によりパラメータの推定値を求めるところまでが自動化できました。

次にバイアスを求めるために、平均対数尤度を求めます。平均対数尤度を求めるためには真の確率分布が必要で、通常は真の確率分布は分からない(だから推定したい)のですが、ブートストラップ法では観測値の経験分布を真の分布だとみなします。
ガス濃度が1.6907の行に関しては、ブートストラップ標本から推定した確率がH4セルの値ですので、確率変数の値が1ならば対数尤度はlog(H4)、確率変数の値が0ならば対数尤度はlog(1-H4)です。そして確率6/59で1、確率53/59で0になりますから、期待値は
6/59*log(H4)+53/59*log(1-H4)
です。対数尤度を用いて推定するのは平均対数尤度の標本数倍ですので、この行なら59倍して
6*log(H4)+53*log(1-H4)
が推定したい値となります。これを各行で計算して足したものと比較して、対数尤度がどれくらい大きいか、その期待値が、問題のバイアスです。

これを100回繰り返して、対数尤度－平均対数尤度を100回足して100で割ったものが、バイアスのブートストラップ推定量です。
大体2前後になるはずです。
Sub bootstrap()
bias = 0
For i = i To 100
　For j = 4 To 11
　　wa = 0
　　For k = 1 To Cells(j, 2)
　　　If Rnd() < Cells(j, 3) / Cells(j, 2) Then
　　　　wa = wa + 1
　　　End If
　　Next k
　　Cells(j, 7) = wa
　Next j
　Application.Run "Solver.xla!Auto_Open"
　SolverOk SetCell:="$I$12", MaxMinVal:=1, ValueOf:="0", ByChange:="$I$1:$I$2"
　SolverSolve Userfinish:=True
　bias = bias + Cells(12, 9) - Cells(12, 10)
Next i
Cells(13, 10) = bias / 100
End Sub

また、ブートストラップ標本を作るのに、確率として死亡数/かぶと虫総数の代わりに推定したパラメータから求めた値(E列)を用いる方法をパラメトリックブートストラップ法と言います。