準備
左上のファイルからオプションを選びます。
アドインを選んで下の設定を押します。
ソルバーアドインと分析ツールにチェックを付けます。
データ
皆さんが持っている教科書のデータを、一つ一つ入力していると時間がかかりますので、あらかじめ書いておきました。| 例1.1 | 例1.2 | 例1.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
出典 |
ヒストグラム
例1のデータのヒストグラムを書きましょう。例1のデータをエクセルのA列にコピーしてください。
統計学IIの講義で説明するように、95~105, 105~115,...,165~175の区間に分けます。
区間の境界となる105,115,...,165をC列に書きます。
データからデータ分析を選びます。
データ分析からヒストグラムを選びます。
入力範囲欄に観測値を入力したセルを、データ区間欄に区間の境界を書いたセルを指定し、
出力先は少し右隣のE1セルを指定します。
右下のグラフ作成にもチェックを付けてOKを押します。
すると度数分布表とヒストグラムが出来上がります。
このままではx軸の表記がおかしいです。105と書かれた部分は95~105ですし、次の級と書かれた部分は165~175です。そこで各区間の中心値をD列に書いて、これをx軸に使います。
D列のデータをx軸に使うために、グラフを右クリックしてデータの選択を選びます。
右側の横(項目)軸ラベルの編集を押します。
D列に書いた数字を指定します。
これで、横軸に中心値が表示されました。
一種類しかないのに右側に説明がつくのは邪魔ですので消します。
このヒストグラムでは、102と104の人は同じ縦棒に含まれるのに、104の人と106の人は遠くに離れてしまっていますので、棒をくっつけます。
棒の上で右クリックして、データ系列の書式設定を選びます。
要素の間隔をなし(左側)にします。
これで完成です。あとは見やすい大きさに調整してください。
データの特性値
Sheet2に切り替えて、例1.2のデータをA1セルから貼り付けてください。Excelを使って、教科書の例1.2, 例1.4の計算をします。
合計値と代表値を計算します。 B1セルに合計値と書いて、C1セルに =SUM(A1:A30)と書いてください。 B2セルに平均値と書いて、C2セルに =AVERAGE(A1:A30)と書いてください。 B3セルに中央値と書いて、C3セルに =MEDIAN(A1:A30)と書いてください。
次に散布度を計算します。エクセルの参考書で分散を調べるとVARと書かれていますので、
B4セルに分散と書いて、C4セルに =VAR(A1:A30)と書いてください。
すると19.75…と表示されます。
教科書例1.4では19.09となっていますので、計算誤差にしては違いが大きすぎます。
理由は、このVAR関数は不偏分散
を計算しているからです。
これは教科書第4章で、母集団分布の分散を推定するために計算した式です。
教科書第1章では、推定ではなくデータそのものの分散を計算するので
を計算します。
B4セルに先ほど書いた分散を不偏分散に修正して、
B5セルに標本分散と書いて、C5セルに =VARP(A1:A30)と書いてください。
標準偏差も同様に二種類あります。
B6セルに標準偏差と書いて、C6セルに =STDEV(A1:A30)と書いてください。
B7セルに標本標準偏差と書いて、C7セルに =STDEVP(A1:A30)と書いてください。
その他の特性値としては
B8セルに平均偏差と書いて、C7セルに =AVEDEV(A1:A30)と書いてください。
B9セルに最小値と書いて、C7セルに =MIN(A1:A30)と書いてください。
B10セルに最大値と書いて、C7セルに =MAX(A1:A30)と書いてください。
2変量の相関
Sheet3に切り替えて例1.6のデータをA1セルから貼り付けてください。 散布図を描きましょう。B2セルの上でマウスの左ボタンを押して、押したままC21セルまでマウスを移動させて左ボタンを離します。
そして画面上の「挿入」から「散布図」の「散布図(マーカーのみ)」を選びます。
すると図のような散布図が得られます。マウスを合わせるとそれが何番目のデータで、x,yの値が何であるか表示されます。
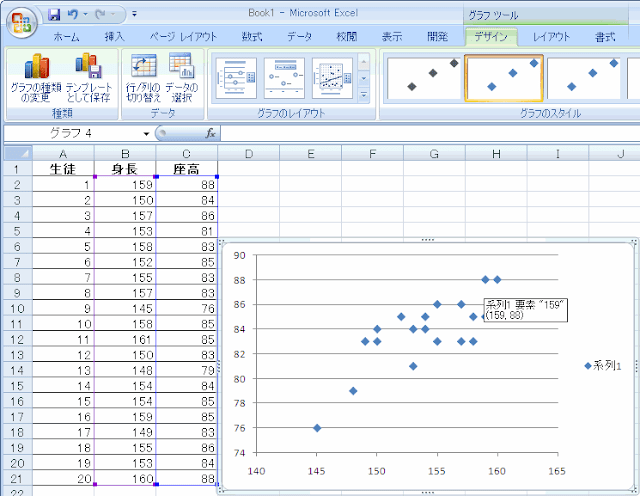
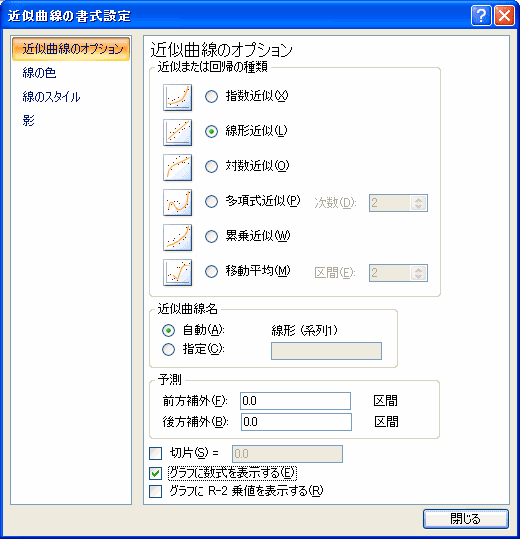
次に回帰直線をExcelに書いてもらいましょう。データ点のどれかにマウスを合わせて右ボタンを押して、表示されるメニューから「近似曲線の追加」を選びます。
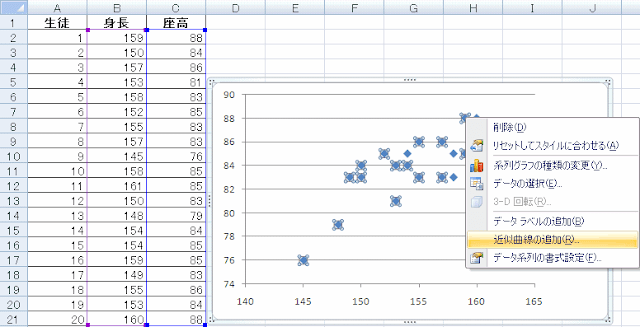
「近似または回帰の種類」は「線形近似」を選び、また式も見たいので、「グラフに数式を表示する」にチェックをつけて、閉じるをクリックすると、回帰直線とその式が表示されます。
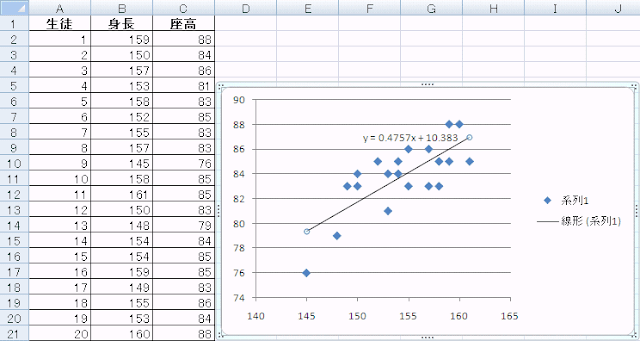
さてこの係数0.4757や定数10.383はどうやって求めましたか？
データを, 直線を
とおくと、
から計算したyの値は
、
これと実際のyの値
との差
を2乗して正の値にしてから足した
を最小にするのでしたね。a,bに関して2次関数で非負ですから必ず最小値を持つので、a,bで偏微分してそれぞれ0とおけばa,bに関する2元連立1次方程式になるのでそれをa,bについて解くことで
と求めることが出来ます。但しはそれぞれ
や
の平均、つまり
です。
ソルバー
もっと複雑な問題を考える時は
座高の推定
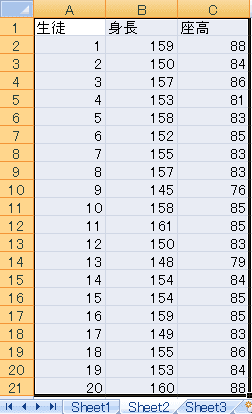
y=ax+bのaとbを、Excelに直接計算させます。そのためにまずaやbの値を書く場所を用意しておきますのでA23セルに「a」、A24セルに「b」と書いてB23セルにaの値、B24セルにbの値を書くことにします。
空っぽだと数字にならないので何か適切な値を書いておきます。全く見当がつかないので、真横の線を書くことにしてaは傾きなので0、bは座高の大体の平均84にしておきます。
このaとbを用いて、y=ax+bという式を用いて身長から座高を推定しますので、D1セルに「座高の推定値」、D2セルに身長とa,bから推定した1番目の生徒の座高の式を書きます。y=ax+bなので「=B23*B2+B24」ですが、D3～D21にコピーしますからa,bを示すB23, B24が変わらないように「=B$23*B2+B$24」と書いておいて、それをコピーします。
当たり前ですが、真横の線で推定したので全て84です。
推定の様子をグラフに書いてみましょう。まず身長、座高、座高の推定値のデータを選択して散布図を描きます。
推定値の方は直線にしたいので推定値の点を右クリックして「データ系列の書式設定」を選びます。
「線の色」は「線(単色)」、「マーカーの種類」は「なし」を選んで「閉じる」をクリックします。
するとグラフがこのようになりますので、B23, B24セルの数字を変化させて直線が点に近付くように調整してみてください。
a=0.5, b=7だとこんな感じです。
あてはまりの良さの評価
見た目で評価したのでは不正確ですので、数値的に評価しましょう。推定値がどれくらいずれているか計算するために、E1セルに「推定誤差」と書いて、E2セルに推定値と実際の座高の差「=D2-C2」を書いて、その式をE21までコピーします。
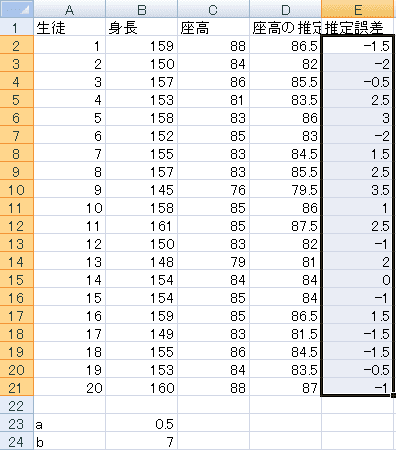
誤差はプラスにもマイナスにもなるので、そのまま合計、平均を求めると打ち消しあってしまいます。だから二乗してから足し算します。
F1セルに「誤差の二乗」と書いて、F2セルに誤差を二乗した「=E2^2」と書いてF21セルまでコピーします。最後にF22に、その20個の誤差の二乗を合計する式「=SUM(F2:F21)」を書きます。
このF22の値が誤差平方和で、この値が小さいほどあてはまりが良いことになります。この値を小さくするようにa,bの値を調整します。
ソルバーの利用
a,bの値を自分で調整していては大変ですし不正確ですから、Excelに調整させましょう。「データ」を選んで右端の「ソルバー」をクリックします。
どのセルをどうしたいのか(最大にする、最小にする)、そのためにどのセルの値を変化させるのか、を尋ねられますので、今回は誤差平方和であるF22を最小にするためにB23からB24までのセルを変化させると入力して「実行」をクリックします。
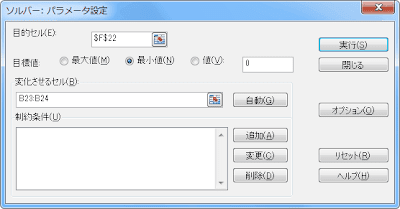
すると最小にする値を求めてくれます。
0 件のコメント:
コメントを投稿