環境数理学科出身の受講生の皆さんにとっては復習だと思います。
準備
Windowsの場合いきなり
このように文字化けしていますので、
GUIプリファレンスを選んで
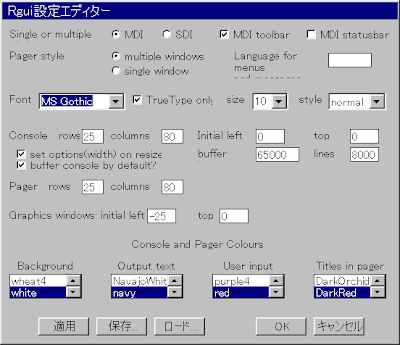
FontをMS Gothicにして、保存を選んで設定をファイルに保存してからOKを押します。
変数の扱い方
>と表示されているところで
a=1
と入力してEnterを押すとaに1が代入されます。確認するには
a
と入力してEnterを押すと
[1] 1
と表示されます。[1]は1番目の要素ということです。
複素数も
a=1+1i
のように書いて扱うことが出来ます。1+iではないことに注意してください。単独のiは変数名として扱われます。
ベクトルはc(要素)と書きます。例えば
b=c(10,20,30)
と書けば、ベクトル(10,20,30)になります。
ベクトルは特に指定しなければ縦ベクトルになりますが、横ベクトルでなければ都合が悪いときは勝手に転置してくれます。
スカラーの場合と同じように確認すると
[1] 10 20 30
と表示されます。
1,2,...,100のような列なら
c=1:30
と書きます。これを確認すると
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
[21] 21 22 23 24 25 26 27 28 29 30
のように表示されます。[21]は折り返して表示された一番左が21番目の要素ということです。
要素を取り扱うには[]を使います。例えば
b[2]
と確認すると
[1] 20
ですし、
b[2]=200
と代入してから
b
を確認すると
[1] 10 200 30
となります。
複数の要素を扱うには、[]の中にベクトルを書きます。例えば1番目と3番目の要素なら
b[c(1,3)]
[1] 10 30
です。また負の数を指定すると、それを除いた他の要素になります。
b[-2]
[1] 10 30
ベクトルの定義の方法には他にも色々ありますが、詳しくは左の欄の教科書を見てください。
行列の定義の方法も色々ありますが、見た目で分かりやすいのはベクトルを並べることでしょう。
c=rbind(c(1,2,3),c(4,5,6),c(7,8,9))
とすると、各ベクトルをrowベクトル(行ベクトル)として並べて行列を作ります。一方
d=cbind(c(1,2,3),c(4,5,6),c(7,8,9))
とすると、各ベクトルをcolumnベクトル(列ベクトル)として並べて行列を作ります。
行列の成分の指定方法は、いちいち列挙すると大変なので例を並べます。
|
コマンド |
機能 |
|
c[2, ] |
2 行目を取り出す |
|
c[ ,2] |
2 列目を取り出す |
|
c[1, 2] |
1 行 2 列目の成分を取り出す |
|
c[c(1,2), 2] |
1,2 行 2 列目の成分を取り出す |
|
c[c(1,2), c(1,3)] |
1, 2 行目と 1, 3 列を取り出す |
|
c[ ,-c(1, 3)] |
1, 3列を除外した行列を取り出す |
演算
+,-は普通の演算と同じです。但し、ベクトル、行列の型がそろっていない場合、エラーにならず足りないほうを繰り返し使ってくれます。
ですから、例えば行列cの全ての成分に1を足したいなら
c+1
だけで出来ます。
*,/は成分ごとの掛け算、割り算になります。型がそろっていない場合の対応は足し算、引き算と同じです。
行列の掛け算は %*% です。この場合はちゃんと行列の型が揃っていないとエラーになります。
行列cの転置行列はt(c), 逆行列はsolve(c)です。連立一次方程式を解くということでsolveなのでしょう。
計算練習
さてここまで準備しておけば、昨年度のこの講義の最後の課題 環境データ解析の例も簡単に解くことが出来ます。このデータを全部入力していると大変ですから、ホームページからコピーしたいのですが、InternetExplorerでは表の区切りがタブにならないので、MozillaかFirefoxで開いてください。
- パソコンにmozillaやFirefoxがインストールされている場合
この表を、一番上の項目名も含めてコピーしてから、Rでindex city y x1 x2 x3 1 稚内 -8.0 45.42 141.68 2.8 2 旭川 -13.6 43.77 142.37 111.9 3 札幌 -9.5 43.05 141.33 17.2 4 青森 -5.4 40.82 140.78 3.0 5 盛岡 -6.7 39.70 141.17 155.2 6 仙台 -3.2 38.27 140.90 38.9 7 金沢 -0.1 36.55 136.65 26.1 8 長野 -5.5 36.67 138.20 418.2 9 高山 -7.6 36.15 137.25 560.2 10 軽井沢 -10.0 36.33 138.55 999.1 11 名古屋 -0.9 35.17 136.97 51.1 12 飯田 -4.7 35.52 137.83 481.8 13 東京 -0.4 35.68 139.77 5.3 14 鳥取 0.5 35.48 134.23 7.1 15 京都 -0.6 35.02 135.73 41.4 16 広島 0.2 34.37 132.43 29.3 17 福岡 1.5 33.58 130.38 2.5 18 鹿児島 2.0 31.57 130.55 4.3 19 高知 0.1 33.55 133.53 1.9 20 那覇 13.5 26.23 127.68 34.9
data1=read.delim("clipboard", sep="\t")
と入力すると、コピーしたデータがdata1に貼り付けられます。 - パソコンにInternetExplorerしか入っていない場合
表を何らかの方法でCSVファイルとして保存します。上の表を表計算ソフトに貼り付けてCSVファイルとして保存するか、下のテキストをエディタに貼り付けてdata.csvというファイル名で保存してください。
保存したらindex,city,y,x1,x2,x3
1,稚内,-8,45.42,141.68,2.8
2,旭川,-13.6,43.77,142.37,111.9
3,札幌,-9.5,43.05,141.33,17.2
4,青森,-5.4,40.82,140.78,3
5,盛岡,-6.7,39.7,141.17,155.2
6,仙台,-3.2,38.27,140.9,38.9
7,金沢,-0.1,36.55,136.65,26.1
8,長野,-5.5,36.67,138.2,418.2
9,高山,-7.6,36.15,137.25,560.2
10,軽井沢,-10,36.33,138.55,999.1
11,名古屋,-0.9,35.17,136.97,51.1
12,飯田,-4.7,35.52,137.83,481.8
13,東京,-0.4,35.68,139.77,5.3
14,鳥取,0.5,35.48,134.23,7.1
15,京都,-0.6,35.02,135.73,41.4
16,広島,0.2,34.37,132.43,29.3
17,福岡,1.5,33.58,130.38,2.5
18,鹿児島,2,31.57,130.55,4.3
19,高知,0.1,33.55,133.53,1.9
20,那覇,13.5,26.23,127.68,34.9
data1=read.csv(file.choose())
と入力すると、ファイルを選択する画面になるので、読み込みたいcsvファイルを指定してください。
data1$x1
として取り扱うことが出来ます。
読み込めたら、実際にデータ解析してみましょう。
このデータは、20地点の1月の日最低気温の月平均値y, 緯度x1, 経度x2, 標高x3のデータです。この緯度、経度、標高と気温の関係を数式で表したいと思います。 また神戸の緯度は34.68、経度は135.18、標高は59.30です。神戸の気温を推定しましょう。
緯度、経度、標高と気温の関係は色々考えることが出来ますが、今回は緯度、経度、標高の3変量を使う最も簡単なものとして
y=β0+β1x1+β2x2+β3x3+誤差
という形を考えます。
β0,β1,β2,β3はどうやって決めましょうか。
本当の気温yと、緯度、経度、標高から推定した気温β0+β1x1+β2x2+β3x3
との差が小さくなるように決めましょう。
データの
1番目の都市の気温をy1、緯度をx11、経度をx12、標高をx13
2番目の都市の気温をy2、緯度をx21、経度をx22、標高をx23
・・・・・
20番目の都市の気温をy20、緯度をx20,1、経度をx20,2、標高をx20,3
と書きます。すると、本当の気温と推定した気温の差は
y1-(β0+β1x11+β2x12+β3x13)
y2-(β0+β1x21+β2x22+β3x23)
・・・・・
y20-(β0+β1x20,1+β2x20,2+β3x20,3)
です。これらはプラスになったりマイナスになったりするので、そのまま足すと打ち消しますから、二乗して足して
∑i=120 {yi-(β0+β1xi1+β2xi2+β3xi3)}2
が最小になるようなβ0,β1,β2,β3を求めることにします。
一見、求めるのは難しそうに見えます。でもこれはβ0,β1,β2,β3に関する二次式で、しかもは二乗して足していますから0以上です。だからグラフは下に凸になっていて、どこかで最小値を取ります。
公式の導出は省略しますが、実は最小にするβ0,β1,β2,β3は次の連立一次方程式を解くことで求めることが出来ます。
まず未知数β0,β1,β2,β3を縦に並べた ベクトル
| β0 |
| β1 |
| β2 |
| β3 |
ベクトル
| y1 |
| y2 |
| ・ |
| ・ |
| y20 |
最後に行列
| 1 | x11 | x12 | x13 |
| 1 | x21 | x22 | x23 |
| ・ | ・ | ・ | ・ |
| ・ | ・ | ・ | ・ |
| 1 | x20,1 | x20,2 | x20,3 |
1が縦に並んでいるのはβ0の係数だからです。この時、最小にするβ0,β1,β2,β3は 連立一次方程式
(Xt・X)Β=(Xt・Y)
を解くことで得られます。Xの右上のtは転置を表します。
この連立一次方程式を解いて、β0,β1,β2,β3を求めてみましょう。
この公式のYは単純に
Y=data1$y
あるいはdata1の3列目ですので
Y=data1[,3]
で得られます。
Xはまず1を縦に20個並べたベクトルが1列目、後はdata1のx1,x2,x3です。
1を20個並べたベクトルを作るには
rep(1, length=20)
とします。よってXは
X=cbind(rep(1, length=20),data1$x1,data1$x2,data1$x3)
あるいは
X=cbind(rep(1, length=20),data1[,c(4,5,6)])
で与えられそうですが、後者のように複数行まとめて取り出すと行列ではなくデータフレームと呼ばれる変数名込みのデータになっているので
X=as.matrix(cbind(rep(1, length=20),data1[,c(4,5,6)]))
とする必要があります。
行列の積は%*%、転置はt( )、逆行列はsolve( )でしたので、上記の公式を使って係数ベクトルβを求めて変数bに代入してください。
また神戸についてはx1=34.68、x2=135.18、x3=59.30でしたので、先頭に1をつけてc(1, 34.68, 135.18, 59.30)をベクトルbに掛けて下さい。約0.23になります。実際の気温は1.2でした。





0 件のコメント:
コメントを投稿