準備
下図のようにメニューを辿ってExcelを立ち上げましょう。
初めて使う時にはいくつか聞かれますので、共にOKを押してください。
左上の丸いボタンを押して、「Excelのオプション」をクリックします。そして左側の「アドイン」をクリックして、下の「管理:Excelアドイン」の横の「設定」をクリックします。
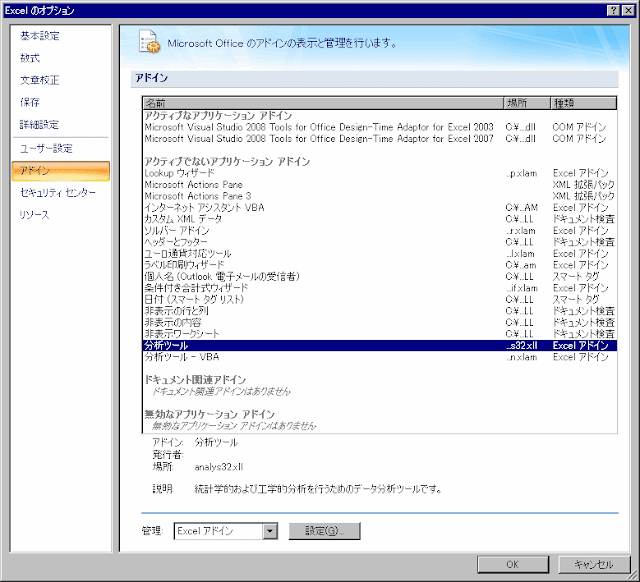
するとアドインの画面に切り替わるので、下のほうの「管理」が「Excelアドイン」になっていることを確かめてその右の「設定」をクリックします。
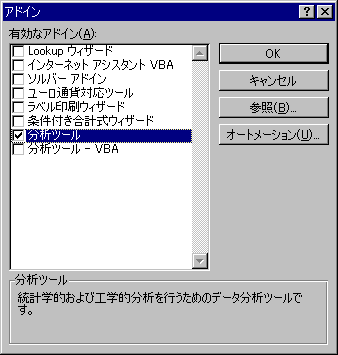
「分析ツール」にチェックをつけてOKをクリックします。
「インストールしますか」と聞かれたら「はい」と答えます。
教科書第一章の例
皆さんが持っている教科書のデータを、一つ一つ入力していると時間がかかりますので、あらかじめ書いておきました。| 例1.1 | 例1.2 | 例1.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
例1.1 度数分布表とヒストグラム
1変量データをエクセルに入力します。キーボードから入力するか、あるいは上の表をコピーして、エクセルに貼り付けます。Internet Explorerを使うときには「コピー」してからExcelで「貼り付け(P)」を選びます。
Firefoxに慣れているのでFirefoxを使いたい!という人は「貼り付け(P)」ではなく「形式を選択して貼り付け(S)」を選んで「テキスト」を選んでください。
次に、階級の境界の数字をC2セル以降に入力します。
右上の「データ分析」をクリックして「ヒストグラム」をクリックしてOKを押します。
以下のように入力してOKを押します。
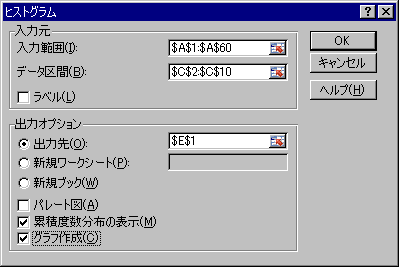
教科書で度数と書かれている部分が、エクセルでは頻度と表示されます。その右には累積相対度数が表示されます。
教科書と同じ結果になりましたか?もし違うなら、その理由を考えてみてください。
例1.2、例1.4 1変量の特性値を求める
エクセル左下のSheet2をクリックして、新しいシートに切り替えます。
そして例1.2のデータをコピーしてA1セルから貼り付けます。A30セルまでデータが30個並んでいるはずです。
まず平均を求めましょう。B1セルに「平均値」と書いてください。
Excelで平均を求める関数はAVERAGEです。C1セルに=AVERAGE(A1:A30)と書いてください。
次に中央値を求めます。B2セルに「中央値」、C2セルに=MEDIAN(A1:A30)を入力します。
次に分散と標準偏差を求めます。まずB3セルに「分散」、B4セルに「標準偏差」と書きます。
第一章では分散を推定するのではなく、単にデータの分散を計算するだけです。このように推定する必要がない場合は分散はVARP、標準偏差はSTDEVPという関数を使いますので、C3セルに=VARP(A1:A30)、C4セルに=STDEVP(A1:A30)と書きます。
ちなみに、推定する場合はVARとSTDEVを使います。
例1.6 2変量の相関を調べる。
エクセル左下のSheet3をクリックして、新しいシートに切り替えて、例1.6のデータをコピーして貼り付けます。特性値
2変量のデータの特性値としては、各々の代表値、散布度の他に、二つの変量の共分散、相関係数があります。D1セルに「共分散」、D2セルに「相関係数」と書いてください。身長のデータはB2からB2に、座高のデータはC2からC21に貼り付けられていますので、E1セルに=COVAR(B2:B21,C2:C21)、E2セルに=CORREL(B2:B21,C2:C21)と書きます。散布図を描きましょう。
B2セルの上でマウスの左ボタンを押して、押したままC21セルまでマウスを移動させて左ボタンを離します。そして画面上の「挿入」から「散布図」の「散布図(マーカーのみ)」を選びます。
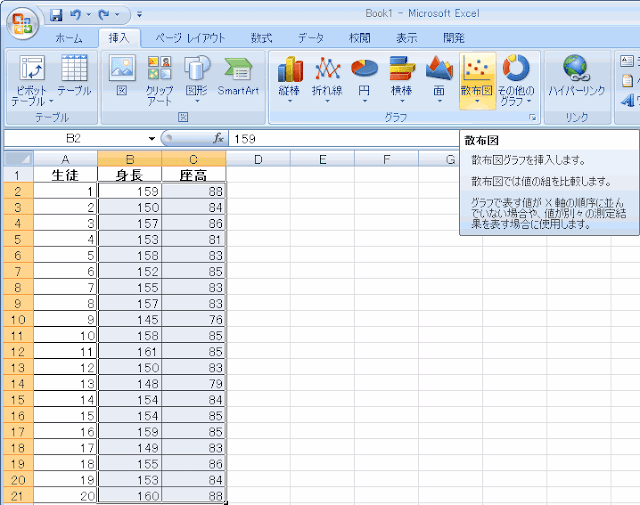
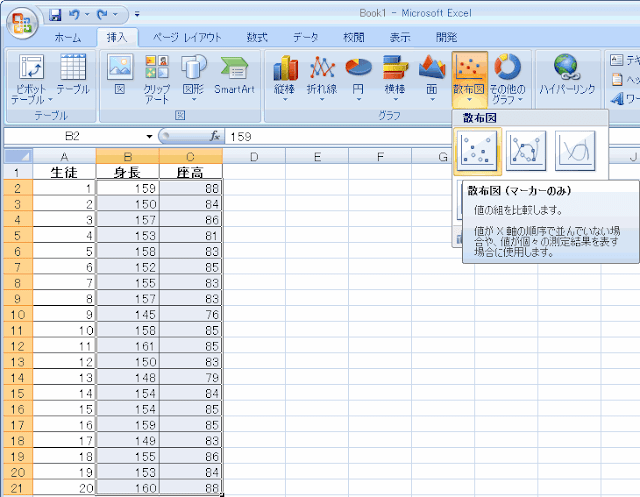
すると図のような散布図が得られます。マウスを合わせるとx,yの値が何であるか表示されます。
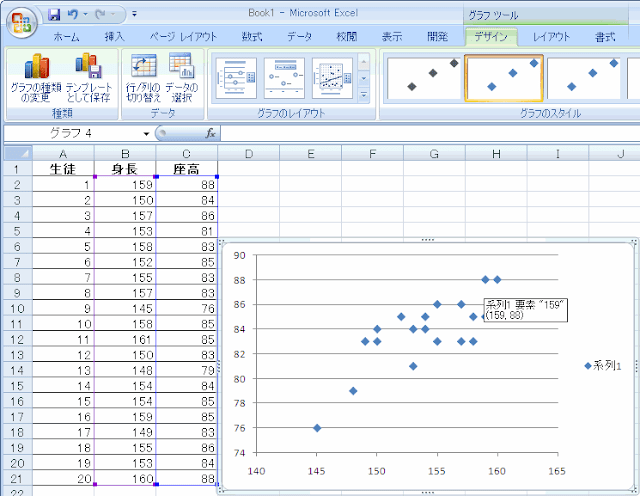
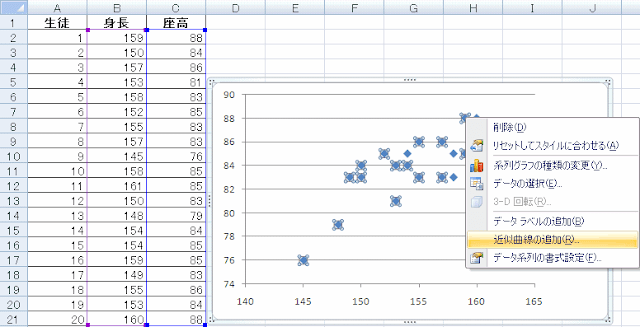
次に回帰直線をExcelに書いてもらいましょう。データ点のどれかにマウスを合わせて右ボタンを押して、表示されるメニューから「近似曲線の追加」を選びます。
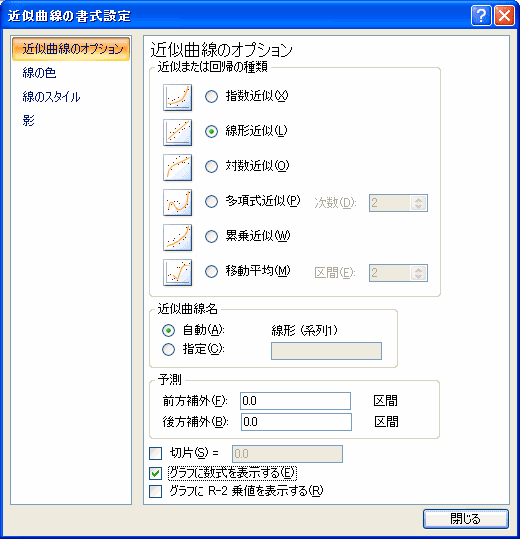
「近似または回帰の種類」は「線形近似」を選び、また式も見たいので、「グラフに数式を表示する」にチェックをつけて、閉じるをクリックすると、回帰直線とその式が表示されます。
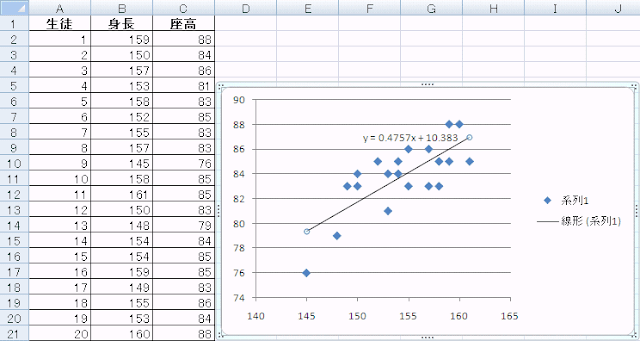
さてこの係数0.4757や定数10.383はどうやって求めましたか?
データを, 直線を
とおくと、
から計算したyの値は
、
これと実際のyの値
との差
を2乗して正の値にしてから足した
を最小にするのでしたね。講義で2週間に渡って説明したように
となります。但しはそれぞれ
や
の平均、つまり
です。
Excelを使った計算練習
実際に計算してみましょう。実はExcelには平均、分散、共分散だけでなく、このような回帰直線の係数を求める機能も備わっていますが、Excelの練習のために合計を求める関数SUMだけを使って、上の式の通りに計算してみましょう。
まず合計を計算します。A22セルに「合計」と書いて、B22セルに「=SUM(B2:B21)」と書きます。これはB2からB21までの数を足し算した値という意味です。

同様にC2からC21までの合計を求める式をC22に書きますが、面倒ですのでB22セルの=SUM(B2:B21)をコピーしてC22セルに貼り付けます。


右に一つずらしてコピーすると=SUM(B2:B21)が=SUM(C2:C21)に変化します。
次に平均を計算しましょう。まずA23セルに「平均」と書きます。B23に、先ほど計算した合計をデータ数20で割った値を書きたいので「=B22/20」と書きます。C23は先ほど同様B23に書いた式をコピーします。

これでを計算できました。
次にを計算します。D1セルに「身長の平均との差」と書きましょう。D2セルには、1番目の生徒の身長B2と身長の平均B23の差を書きたいので「=B2-B23」と書けばとりあえず計算は出来ます。でもD3, D4,...,D21セルにいちいち式を書きたくないのでD2セルの式をコピーしたいです。でもD2セルに「=B2-B23」と書いてから一つ下にコピーすると「=B3-B24」になってしまいます。平均はB23セルですからB24になっては困ります。
「=B2-B23」を下にコピーした時に、B2はB3に変化して欲しいのですがB23はそのままの方が良いです。こんなときは、変わって欲しくない23の前に$をつけて「=B2-B$23」と書きます。すると下にコピーした時に「=B3-B$23」になります。


同様にを計算します。まずE1セルに「座高と平均との差」と書いて、次にE2セルに式を入力するのですが、先ほどD2セルに「=B2-B$23」と入力しているのでこれをコピーして一つ右のE2セルに貼りつけるとBがCに変わって「=C2-C$23」になりますから、書かなくてもコピーすれば良いです。

ここまで入力すると以下のようになっているはずです。

練習:D列の和を計算してみてください。
0になる筈ですが計算機の誤差のために1.14E-13となりました。これはという意味です。ほぼゼロですね。
次はとその合計、平均です。F1セルに「身長の平均との差の2乗」と書いて、F2セルに「=D2^2」と書いてそれをF21セルまでコピーします。そしてF22セルがそれらの合計、F23セルはF22セルを20で割って平均です。するとこうなります。

F23セルの値が身長の標本分散です。
次はとその合計、平均です。G1セルに「身長の平均との差と座高の平均との差の積」と書いて、G2セルに「=D2*E2」と書いてそれをG21セルまでコピーします。そしてG22セルがそれらの合計、G23セルはG22セルを20で割って平均です。するとこうなります。

G23セルが身長と体重の共分散です。
ここまでくればあと一息です。どこでもよいのですが、分かりやすいところということで例えばI3セルに「a」と書いてJ3セルにaの計算式を書いてください。
ですので、分母も分子も既に計算していますね。
同じくI4セルに「b」と書いてJ4セルにbの計算式を書いてください。ですから、右辺の値は既に全部計算しています。
このような値になれば正解です。

先ほどの散布図の式y=0.4757x+10.383と一致していますね。
レポート課題
次のデータは都道府県県庁所在地での2009年の最高気温と最低気温です。| JISコード | 都道府県名 | 最高気温 | 最低気温 |
|---|---|---|---|
| 1 | 北 海 道 | 31.2 | -9.9 |
| 2 | 青 森 県 | 31.8 | -8.9 |
| 3 | 岩 手 県 | 32.3 | -9.6 |
| 4 | 宮 城 県 | 32.8 | -3.8 |
| 5 | 秋 田 県 | 35.5 | -7.4 |
| 6 | 山 形 県 | 35.5 | -7.4 |
| 7 | 福 島 県 | 36.5 | -4.9 |
| 8 | 茨 城 県 | 34.2 | -5.4 |
| 9 | 栃 木 県 | 35.3 | -5.6 |
| 10 | 群 馬 県 | 37.6 | -4.4 |
| 11 | 埼 玉 県 | 35.1 | -4.8 |
| 12 | 千 葉 県 | 33.7 | 0.2 |
| 13 | 東 京 都 | 34.2 | 0.0 |
| 14 | 神奈川県 | 33.3 | 0.4 |
| 15 | 新 潟 県 | 36.3 | -4.1 |
| 16 | 富 山 県 | 35.8 | -3.6 |
| 17 | 石 川 県 | 34.9 | -2.0 |
| 18 | 福 井 県 | 35.3 | -2.5 |
| 19 | 山 梨 県 | 37.0 | -6.9 |
| 20 | 長 野 県 | 35.5 | -8.9 |
| 21 | 岐 阜 県 | 36.9 | -2.9 |
| 22 | 静 岡 県 | 35.9 | -2.6 |
| 23 | 愛 知 県 | 35.2 | -2.0 |
| 24 | 三 重 県 | 36.0 | -1.6 |
| 25 | 滋 賀 県 | 35.6 | -1.8 |
| 26 | 京 都 府 | 36.5 | -1.9 |
| 27 | 大 阪 府 | 36.3 | 0.0 |
| 28 | 兵 庫 県 | 35.1 | 0.4 |
| 29 | 奈 良 県 | 35.4 | -3.5 |
| 30 | 和歌山県 | 34.1 | -1.3 |
| 31 | 鳥 取 県 | 34.8 | -2.5 |
| 32 | 島 根 県 | 34.1 | -3.2 |
| 33 | 岡 山 県 | 35.2 | -2.0 |
| 34 | 広 島 県 | 35.4 | -2.3 |
| 35 | 山 口 県 | 34.9 | -2.8 |
| 36 | 徳 島 県 | 35.1 | -2.0 |
| 37 | 香 川 県 | 35.7 | -0.3 |
| 38 | 愛 媛 県 | 35.1 | -0.1 |
| 39 | 高 知 県 | 36.5 | -2.6 |
| 40 | 福 岡 県 | 34.9 | -1.2 |
| 41 | 佐 賀 県 | 37.8 | -2.5 |
| 42 | 長 崎 県 | 36.5 | -1.2 |
| 43 | 熊 本 県 | 36.1 | -2.6 |
| 44 | 大 分 県 | 35.5 | -2.6 |
| 45 | 宮 崎 県 | 36.7 | -1.8 |
| 46 | 鹿児島県 | 35.7 | 0.2 |
| 47 | 沖 縄 県 | 34.6 | 9.3 |
講義の内容はここまでです。以下は、より発展的な内容です。
時間に余裕のある人、研究において「統計学入門」の範囲を超えるデータ解析が必要になる人のために用意しました。ソルバー
もっと複雑な問題を考える時は準備
左上の丸いボタンを押して、「Excelのオプション」をクリックします。そして左側の「アドイン」をクリックして、下の「管理:Excelアドイン」の横の「設定」をクリックします。
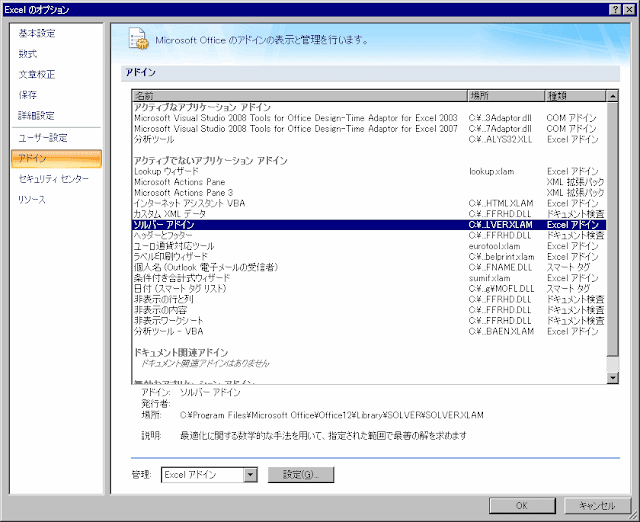
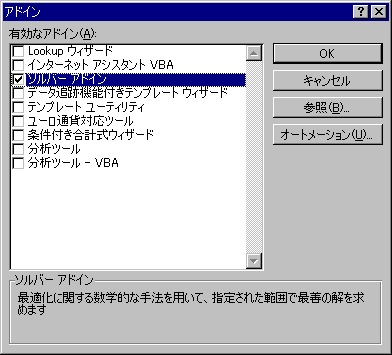
するとアドインの画面に切り替わるので「ソルバーアドイン」にチェックをつけてOKをクリックします。 「インストールしますか」と聞かれたら「はい」と答えます。

座高の推定
先ほどの表には既に色々書き足して分かり辛いので、Sheet3の右をクリックしてSheet4を追加してそれに切り替えてもう一度同じ表をコピーしておきます。
今度はy=ax+bのaとbを、自分で計算した数式を使わず、Excelに直接計算させます。そのためにまずaやbの値を書く場所を用意しておきますのでA23セルに「a」、A24セルに「b」と書いてB23セルにaの値、B24セルにbの値を書くことにします。
空っぽだと数字にならないので何か適切な値を書いておきます。全く見当がつかないので、真横の線を書くことにしてaは傾きなので0、bは座高の大体の平均84にしておきます。
このaとbを用いて、y=ax+bという式を用いて身長から座高を推定しますので、D1セルに「座高の推定値」、D2セルに身長とa,bから推定した1番目の生徒の座高の式を書きます。y=ax+bなので「=B23*B2+B24」ですが、D3~D21にコピーしますからa,bを示すB23, B24が変わらないように「=B$23*B2+B$24」と書いておいて、それをコピーします。

当たり前ですが、真横の線で推定したので全て84です。
推定の様子をグラフに書いてみましょう。まず身長、座高、座高の推定値のデータを選択して散布図を描きます。


推定値の方は直線にしたいので推定値の点を右クリックして「データ系列の書式設定」を選びます。

「線の色」は「線(単色)」、「マーカーの種類」は「なし」を選んで「閉じる」をクリックします。


するとグラフがこのようになりますので、B23, B24セルの数字を変化させて直線が点に近付くように調整してみてください。

a=0.5, b=7だとこんな感じです。

あてはまりの良さの評価
見た目で評価したのでは不正確ですので、数値的に評価しましょう。推定値がどれくらいずれているか計算するために、E1セルに「推定誤差」と書いて、E2セルに推定値と実際の座高の差「=D2-C2」を書いて、その式をE21までコピーします。
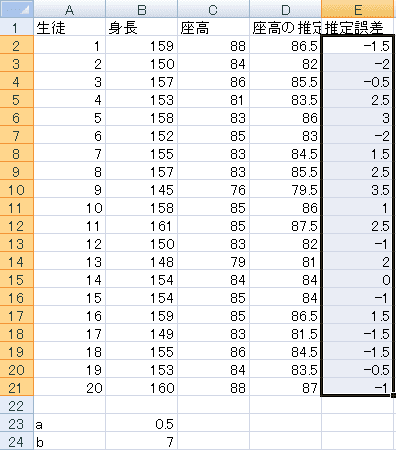
誤差はプラスにもマイナスにもなるので、そのまま合計、平均を求めると打ち消しあってしまいます。だから二乗してから足し算します。
F1セルに「誤差の二乗」と書いて、F2セルに誤差を二乗した「=E2^2」と書いてF21セルまでコピーします。最後にF22に、その20個の誤差の二乗を合計する式「=SUM(F2:F21)」を書きます。

このF22の値が誤差平方和で、この値が小さいほどあてはまりが良いことになります。この値を小さくするようにa,bの値を調整します。
ソルバーの利用
a,bの値を自分で調整していては大変ですし不正確ですから、Excelに調整させましょう。「データ」を選んで右端の「ソルバー」をクリックします。
どのセルをどうしたいのか(最大にする、最小にする)、そのためにどのセルの値を変化させるのか、を尋ねられますので、今回は誤差平方和であるF22を最小にするためにB23からB24までのセルを変化させると入力して「実行」をクリックします。
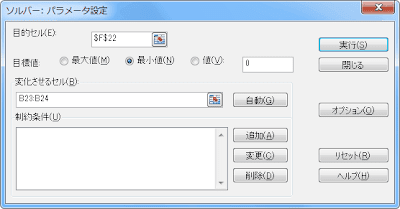
すると最小にする値を求めてくれます。
今回はソルバーを使わなくても直接計算出来る問題でしたので比較してみましょう。
少し値が違いますね。
このようにソルバーには誤差がありますので、今回のように直接計算できる問題の場合は実は使わない方が良いのですが、複雑な問題の場合直接計算できないことがありますので、そのような問題に対してはソルバーは有効です。





0 件のコメント:
コメントを投稿